🎡 [Roformer] RoFormer: Enhanced Transformer with Rotary Position Embedding

🔭 Overview

Roformer는 2021년에 발표된 트랜스포머 모델의 변형으로, RoPE(Rotary Position Embedding)이라는 새로운 위치 정보 포착 방식을 제안했다. 근래 유명한 오픈소스 LLM 모델들(GPT-Neo, LLaMA)의 위치 정보 포착 방식으로 채택 되어 주목을 받고 있다. RoPE 기법에 대해 살펴보기 전에 일단, 관련 분야의 연구 동향 및 위치 정보의 개념에 대해 간단하게 살펴보고 넘어가려 한다.

🤔 Absolute Position vs Relative Position

트랜스포머가 성공을 거둘 수 있었던 이유는 전체 시퀀스를 병렬적으로 한 번에 처리하되, 시퀀스 발생 순서 정보를 행렬합 방식으로 인코딩해줬기 때문이다. 이 분야에 대한 연구 동향은 크게 Absolute Position, Relative Position 방식으로 분화된다.

Absolute Position은 주어진 시퀀스의 길이를 측정한 뒤, 나열된 순서 그대로 forward하게 0부터 길이-1의 번호를 개별 토큰에 할당한다. 다시 말해, 단어가 시퀀스에서 발생한 순서를 수학적으로 표현해 모델에 주입한다는 의미가 된다.

한편, Relative Position은 시퀀스 내부 토큰 사이의 위치 관계 표현을 통해 토큰 사이의 relation을 pairwise하게 학습하는 위치 임베딩 기법을 말한다. 일반적으로 상대 위치 관계는 서로 다른 두 토큰의 시퀀스 인덱스 값의 차를 이용해 나타낸다. 포착하는 문맥 정보는 예시와 함깨 설명하겠다. 예시는 예전 DeBERTa 논문에서 나왔던 것을 활용했다. 딥러닝이라는 단어는 영어로 Deep Learning 이다. 두 단어를 합쳐놓고 보면 신경망을 사용하는 머신러닝 기법의 한 종류라는 의미를 갖겠지만, 따로 따로 보면 깊은, 배움이라는 개별적인 의미로 나뉜다.

• 1) The Deep Learning is the Best Technique in Computer Science
• 2) I’m learning how to swim in the deep ocean

Deep과 Learning의 상대적인 거리에 주목하면서 두 문장을 해석해보자. 첫 번째 문장에서 두 단어는 이웃하게 위치해 신경망을 사용하는 머신러닝 기법의 한 종류 라는 의미를 만들어내고 있다. 한편 두 번째 문장에서 두 단어는 띄어쓰기 기준 5개의 토큰만큼 떨어져 위치해 각각 배움, 깊은 이라는 의미를 만들어 내고 있다. 이처럼 개별 토큰 사이의 위치 관계에 따라서 파생되는 문맥적 정보를 포착하려는 의도로 설계된 기법이 바로 Relative Position Embedding 이다.

🤔 Word Context vs Relative Position vs Absolute Position

줄 서있는 사람들

지금까지 Relative Position Embedding이 무엇이고, 도대체 어떤 문맥 정보를 포착한다는 것인지 알아봤다. 필자의 설명이 매끄럽지 못하기도 하고 예시를 텍스트로 들고 있어서 직관적으로 word context는 무엇인지, Position 정보와는 뭐가 다른지, 두 가지 Position 정보는 뭐가 어떻게 다른지 와닿지 않는 분들이 많으실 것 같다. 그래서 최대한 직관적인 예시를 통해 세가지 정보의 차이점을 설명해보려 한다.

사람 5명이 공항 체크인을 위해 서 있다. 모두 왼쪽을 보고 있는 것을 보아 왼쪽에 키가 제일 작은 여자가 가장 앞줄이라고 볼 수 있겠다. 우리는 줄 서있는 순서대로 5명의 사람에게 번호를 부여할 것이다. 편의상 0번부터 시작해 4번까지 번호를 주겠다. 1번에 해당하는 사람은 누구인가?? 바로 줄의 2번째에 서있는 여자다. 그럼 2번에 해당하는 사람은 누구인가?? 사진 속 줄의 가장 중간에 있는 남자가 2번이다. 이렇게 그룹 단위(전체 줄)에서 개개인에 일련의 번호를 부여해 위치를 표현하는 방법이 바로 Absolute Position Embedding이다.

한편, 다시 2번 사람에게 주목해보자. 우리는 2번 남자를 전체 줄에서 가운데 위치한 사람이 아니라, 검정색 양복과 구두를 신고 손에 쥔 무언가를 응시하고 있는 사람이라고 표현할 수도 있다. 이것이 바로 토큰의 의미 정보를 담은 word context에 해당한다.

마지막으로 Relative Position Embedding 방식으로 2번 남자를 표현해보자. 오른손으로는 커피를 들고 다른 손으로는 캐리어를 잡고 있으며 검정색 하이힐과 베이지색 바지를 입은 1번 여자의 뒤에 있는 사람, 회색 양복과 검은 뿔테 안경을 쓰고 한 손에는 캐리어를 잡고 있는 4번 여자의 앞에 있는 사람, 검정색 자켓과 청바지를 입고 한 손에는 회색 코트를 들고 있는 줄의 맨 앞 여자로부터 2번째 뒤에 서있는 사람, 턱수염이 길고 머리가 긴 편이며 파란색 가디건을 입고 초록색과 검정색이 혼합된 가방을 왼쪽으로 메고 있는 남자로부터 2번째 앞에 있는 사람.

이처럼 표현하는게 바로 Relative Position Embedding에 대응된다고 볼 수 있다. 이제 위치 임베딩에 대해서 살펴봤으니, 논문에서 제시하는 내용에 대해서 알아보자.

🗂️ Previous Work: Relative Position Embedding

미리 말하자면, RoPE는 위치 정보 중에서 상대 위치를 포착한다. 그래서 저자는 그들의 방법론을 소개하기 전에 먼저, 이전 연구들의 상대 위치 포착 방식에 대해서 소개하고 있다. 간단히 살펴보자.

\[q^T_mk_n = x^T_mW^T_qW_kx_n + x^T_mW^T_qW_kp_n + p^T_mW^T_qW_kx_n + p^T_mW^T_qW_kp_n\ \ \ (1) \\\] \[q^T_m k_n = x^T_m W^T_q W_k x_n + x^T_m W^T_q {W_k} \tilde{x}_{m-n} + \widetilde{p}_{m-n} W^T_q W_k x_n \ \ \ (2)\]

(1)번 수식은 Transformer-XL 논문에서 제시된 Cross Attention 수식이다. 위치 정보를 담아내는 항을 따로 만들고 쿼리, 키에 대응되는 항과 곱하고 있다. (2)번 수식은 DeBERTa 모델에서 제시된 Disentangled Attention 이다. (1)과 구성의 차이는 있지만 역시, 위치 정보를 담아내는 항을 억지로 만들고 그것들을 쿼리 혹은 키와 곱하여 위치 정보를 담아낸 뒤, 모두 합하여 어텐션 행렬을 만들어 내고 있다.

정리하면, 기존 연구들은 상대 위치를 포착하기 위해 별도의 포지션 행렬을 만들고, 이리저리 곱하고, 다시 그것들을 모두 합하여 어텐션 행렬을 만들고 있는 것이다. 기존 연구들이 제시하는 방법론들의 공통된 문제는 학습해야 할 파라미터 수가 늘어나 모델 사이즈도 커지고, 학습시간도 늘어난다는 것이다.

🎡 RoPE

\[f_{q,k}(x_m, m)= \left( \begin{array}{cc}\cos(m\theta) & \sin(m\theta) \\-\sin(m\theta) & \cos(m\theta)\end{array} \right) \left( \begin{array}{cc}W^{(11)}_{q,k} & W^{(12)}_{q,k} \\W^{(21)}_{q,k} & W^{(22)}_{q,k} \end{array} \right) \left( \begin{array}{cc}x_m^{(1)} \\x_m^{(2)} \end{array} \right)\]

등식의 좌변은 word embedding을 선형 투영 시켜 얻은 query, key 벡터에 Rotary Position Embedding 값을 추가한 결과 값을 뜻한다. 우변의 수식이 상당히 복잡해 보이나, 실상은 매우 간단하다. 선형 투영으로 얻은 query, key 벡터에 좌측의 괴랄하게 생긴 행렬을 곱해주겠다는 것이다. 좌측의 행렬은 대학교 선형대수 시간에 스치듯 지나갔던 Transformation Matrix(회전 행렬)이다. $m$은 $m$-th 토큰을 의미하는데, 세타가 뭔지는 모르겠지만 일단 토큰의 인덱스 값에 따라서, 주어진 워드 임베딩 벡터를 회전시키겠다는 것이다. 지금 살펴본 예시는 은닉층 크기가 2차원인 단순한 벡터였다. 실제 모델에 사용하는 차원(384, 512, 768, …)으로 확장하기 전에 세타의 정체에 대해 알아보자.

\[\Theta = \left\{ \theta_i = 10000^{ -{2(i-1)}/{d}}, \quad i \in \left[1, 2, \ldots, \frac{d}{2}\right] \right\}\]

$\theta$의 정체는 바로 주기함수 였다. 퓨어한 트랜스포머에서 Absolute Position Encoding을 위해 Sinusoidal 함수를 사용한 것과 같은 이치라고 생각하면 된다. 즉 $\theta$는 word embedding 벡터가 가진 은닉층 차원 방향 인덱스에 따라서 달라진다. 여기에 시퀀스 길이 차원 방향의 인덱스 값을 따로 곱해주기 때문에 그 유일성을 보장할 수 있다.

이제 전체 RoPE를 이해하는데 필요한 재료 준비는 모두 끝났다. 이제 실제 차원으로 확장해보자.

\[fq,k(x_m,m)=R^d_{Θ,m}W_{q,k}x_m \\\]

행렬 $R^d_{Θ,m}$은 아래와 같은 행렬을 말하는데,

\[R^d_{Θ,m} = \begin{bmatrix} \cos(m\theta_1) & -\sin(m\theta_1) & 0 & 0 & \cdots & 0 & 0 \\ \sin(m\theta_1) & \cos(m\theta_1) & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos(m\theta_2) & -\sin(m\theta_2) & \cdots & 0 & 0 \\ 0 & 0 & \sin(m\theta_2) & \cos(m\theta_2) & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos(m\theta_{d/2}) & -\sin(m\theta_{d/2}) \\ 0 & 0 & 0 & 0 & \cdots & \sin(m\theta_{d/2}) & \cos(m\theta_{d/2}) \end{bmatrix}\]

토큰의 인덱스와 모델의 은닉차원 인덱스에 따라서 행렬의 원소값이 결정됨을 알 수 있다. 이제 다시 (3)번 수식의 의미를 생각해보자. 단어 임베딩을 쿼리, 키 행렬로 선형 투영한 뒤 (4)번 수식을 곱한다. 순수한 회전행렬을 쿼리, 키 벡터에 곱하기 때문에 벡터의 크기를 유지한채, 방향만 바꿔줄 수 있다는 장점이 있다.

이전의 연구들은 포지션 정보를 가지고 있는 행렬을 단어 벡터에 더하기 때문에 벡터의 방향은 물론 크기 역시 왜곡된다. 물론 단어 벡터와 포지션 벡터가 서로 성격이 다른 정보라는 점을 고려하면 모델의 은닉층처럼 고차원 공간에서 서로 직교할 확률이 매우 높기 때문에, 서로 학습에 영향을 미칠 가능성은 낮다. 하지만 확률적인 접근일 뿐더러, 단어 벡터의 크기가 왜곡된다는 점이 층을 거듭할수록 영향을 미칠지 알 수 없다.

RoPE 방식의 또다른 장점은 곱하는 것만으로도, 상대 위치 정보를 인코딩 해줄 수 있다는 점이다. 이전 연구들은 대부분 절대 위치 혹은 상대 위치 하나만을 선택해 단어 임베딩에 정보를 추가해주는 경우가 대다수 였다. DeBERTa의 경우에만, Task 레이어 근처(레이어 후반부)에 가서 절대 위치를 더해 상대 위치가 갖는 단점을 보완하려는 시도를 했다. DeBERTa가 여러 방면에서 상당히 좋은 성능을 거둬서 그렇지, 마지막 레이어 근처에 가서 절대 위치를 더해주는게 사실 자연스럽다고 생각되지는 않는다. 그런데 RoPE는 회전 행렬을 곱하는 것만으로도 절대 위치와 상대 위치 모두 인코딩이 가능하다. 어떻게 그럴까??

일단 RoPE 선형 투영된 쿼리, 키 행렬에 각각 회전행렬을 곱한다. 곱하는 과정에서 이미 토큰의 인덱스 값에 따라서 서로 다른 포지션 값이 단어 임베딩에 곱해지게 된다. 이것으로 일단 절대 위치 정보를 추가해줄 수 있다. 그리고 잘 알다시피, 쿼리와 키의 내적을 수행한다. 쿼리와 키의 내적을 각각 단어 임베딩, 선형 투영, 회전행렬 항으로 나눠서 식을 풀어 쓰면 아래와 같다.

\[q^T_mk_n=(R^d_{Θ,m}W_{q}x_m)^T(R^d_{Θ,n}W_{k}x_n) \ \ \ (5)\]

수식을 전개하면 자연스레,

\[x^TW_qR^d_{Θ,n-m}W_kx_n \ \ \ (6)\]

(6)번 수식처럼 된다. 행렬 $R^d_{Θ,n-m}$의 원소는 아래처럼,

\[\cos(m\theta_1)*\cos(n\theta_1) - \sin(m\theta_1)*\sin(n\theta_1) \\\]

토큰 인덱스를 의미하는 $m,n$에 대한 수식으로 표현된다. 따라서 자연스럽게 상대 위치를 포착할 수 있게 된다. 상당히 자연스럽게 서로 다른 두 위치 정보를 인코딩하는게 가능하며, 추가적으로 다른 항을 만들어 어텐션 행렬을 계산하지 않기 때문에 메모리를 좀 더 효율적으로 사용 가능하다.

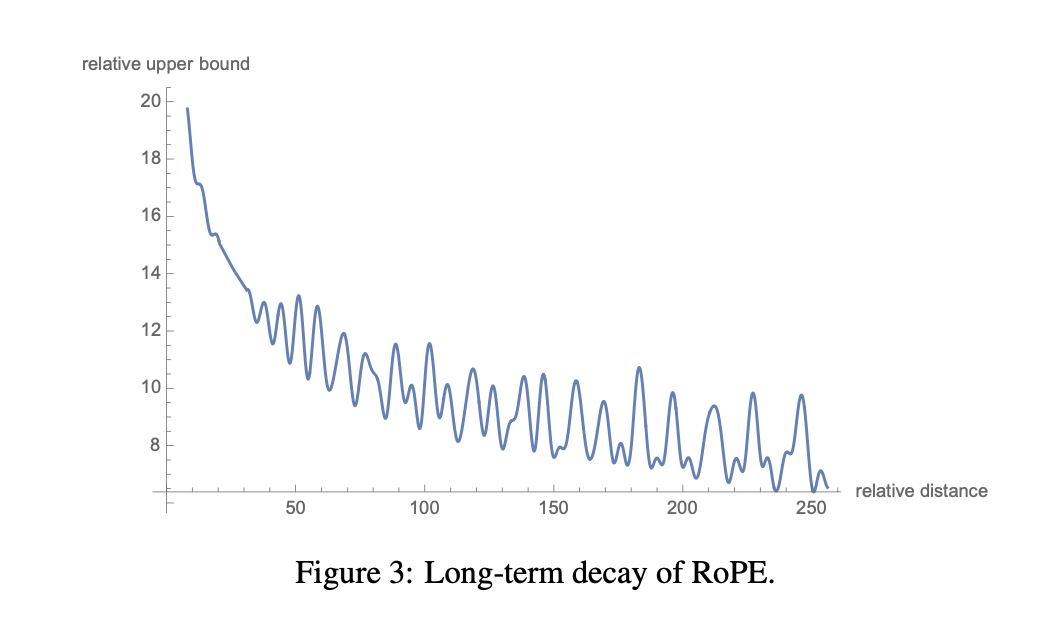
한편, 토큰의 상대 위치를 포착하는 방식은 자신과 상대적 거리가 멀어질수록 의미적 연관성이나 관계성이 떨어진다는 점을 전제로 한다. 즉, 서로 거리가 먼 토큰일수록 쿼리와 키벡터의 내적값이 0에 가까워져야 한다는 것이다. 저자 역시 이점을 언급하며 RoPE 방식이 Long-Term Decay 속성을 갖고 있다고 주장한다.

Long-Term Decay

Appendix에서 수학적으로 증명까지 제시하고 있으나, 필자의 수학 실력이 얕아서 제시된 과정이 이해가 가질 않는다. 추후에 관련 내용은 추가하도록 하겠다. 일단 Relative Upper Bound가 정확히 무엇을 말하는지 모르겠지만(논문에 제대로 언급 x, 추측하건데, 의미적 연관성을 나타내는 지표 같음, 아마 내적값으로 추정), 제시된 그래프를 보면 서로 상대적 거리가 멀어질수록 해당 지표가 확연히 감소하는 추세를 보인다.

마지막으로 논문에서 밝히길 (4), (5)번 수식의 형태로 RoPE를 만드는 것은 연산 효율이 떨어진다고 한다. 그래서 Appendix에서 효율적으로 연산하는 수식을 다시 제시하고 있다.

\[R^d_{Θ,m}x = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_{d-1} \\ x_{d} \\ \end{bmatrix} \otimes \begin{bmatrix} cos (m\theta_1) \\ cos (m\theta_1) \\ cos (m\theta_2) \\ cos (m\theta_2) \\ ... \\ cos (m\theta_{d/2}) \\ cos (m\theta_{d/2}) \\ \end{bmatrix} + \begin{bmatrix} -x_2 \\ x_1 \\ -x_4 \\ x_3 \\ ... \\ -x_{d-1} \\ x_d \\ \end{bmatrix} \otimes \begin{bmatrix} \sin(m\theta_1) \\ \sin(m\theta_1) \\ \sin(m\theta_2) \\ \sin(m\theta_2) \\ \vdots \\ \sin(m\theta_{d/2}) \\ \sin(m\theta_{d/2}) \end{bmatrix}\]

수식 (4), (5)번 형태 그대로 구현하려면, 크기가 [seq_len, dim_head, dim_head]인 텐서를 계속 가지고 있어야 한다. 이는 상당히 메모리를 낭비하게 된다. 아래 그림은 필자가 (4), (5)번 형태 그대로 구현한 뒤, MLM 학습을 돌리던 모습이다.

[body ver result]

11시간 40분으로 훈련 시간이 예측되는걸 볼 수 있다. 물론, 이러한 결과가 나온 이유는 \(R^d_{Θ,m}x\)이 차지하는 메모리 크기가 커지면서, GPU 상에 한 번에 올릴 수가 없어져 배치마다 루프를 돌려서 RoPE를 개별 쿼리, 키에 곱해주는 방식을 선택했기 때문이다. 이제 Appendix에서 제시한 방법대로 RoPE를 구현하면,

[appendix ver result]

이렇게 4시간으로 시간이 드라마틱하게 줄어들었다. 이 방법은 또한 $R^d_{Θ,m}$를 [seq_len, dim_head] 크기를 갖는 텐서를 사용하면 되기 때문에, 이전 방식보다 훨씬 메모리도 덜 차지한다. 이 방식은 배치 차원으로 루프를 돌릴 필요가 없어져 훈련시간도 대폭 단축되는 것이다.

📏 RoPE with linear attention

저자는 퓨어한 full attention 대신 <Transformers are RNNs: Fast Autoregressive Transformers with linear attention> 논문에서 제시된 linear attention 을 사용했다고 밝히고 있다.

하지만, linear attention 의 경우 디코더의 CLM 수행에 어울리는 방식으로, NLU를 위한 인코더에는 적합하지 않다. 해당 논문에서도 모델의 벤치마크 결과를 모두 NLG에 대해서만 제시한다. 그리고 필자가 직접 구현해 MLM을 수행해본 결과(실험 결과 링크) 정확도가 상당히 낮게 나오는 것을 알 수 있다. 물론 애초에 해당 방식은 트랜스포머를 RNN처럼 시간 차원에 대해서 학습하는 경우를 상정하고 만들었기 떄문에 linear attention 을 BERT 같은 인코더 모델에 그대로 사용하는게 애초에 안 맞을 수 있다. 하지만 허깅 페이스의 roformer 코드를 보면 역시, linear attention 대신 full attention에 RoPE를 통합하는 방식으로 구현했다. 따라서 필자 역시 full attention을 기준으로 모델을 구현했음을 밝힌다.

👩‍💻 Implementation by Pytorch

논문의 내용과 오피셜로 공개된 코드를 종합하여 파이토치로 Roformer를 구현해봤다. 다만, linear attention 대신 full attention을 사용했고 오직 인코더 부분만 구현했음을 밝힌다.

한편, 필자가 직접 구현한 RoPE를 코드도 있으나, GPU 연산 최적화까지는 실패해 대신 허깅페이스의 구현체를 참고했음을 밝힌다. 시간이 될 때, 직접 구현했던 RoPE 코드도 함꼐 첨부하겠다. 그리고 이번 포스팅에서는 RoPE를 구현하는 방법에 대해서만 다루고, 나머지 구현에 대한 설명은 생략하려 한다. 전체 모델 구조 대한 코드는 여기 링크를 통해 참고바란다.

🎡 Rotary Position Embedding

_init_weight()의 position_enc를 주목해보자. position_enc는 position과 dim을 인자로 받아 position과 dim에 따라서 position_enc를 만들어내는데, 이것이 바로 RoPE의 핵심이다. 해당 코드 라인이 정확하게 $m\theta_d$을 계산하게 된다.

class RoFormerSinusoidalPositionalEmbedding(nn.Embedding):
    """ This module produces sinusoidal positional embeddings of any length
    Original Source code from Huggingface's RoFormer model, which is the most optimized way to create positional embedding

    Args:
        max_seq: max sequence length of model
        dim_head: dimension of each attention head's hidden states

    Returns:
        Tensor -> torch.Size([seq_len, dim_head])

    References:
        https://arxiv.org/abs/2104.09864  # RoFormer: Enhanced Transformer with Rotary Position Embedding
        https://github.com/huggingface/transformers/blob/main/src/transformers/models/roformer/modeling_roformer.py#L323
    """

    def __init__(self, max_seq: int, dim_head: int) -> None:
        super().__init__(max_seq, dim_head)
        self.weight = self._init_weight(self.weight)

    @staticmethod
    def _init_weight(out: nn.Parameter) -> nn.Parameter:
        """
        Identical to the XLM create_sinusoidal_embeddings except features are not interleaved. The cos features are in
        the 2nd half of the vector. [dim // 2:]
        """
        n_pos, dim = out.shape
        position_enc = np.array(
            [[pos / np.power(10000, 2 * (j // 2) / dim) for j in range(dim)] for pos in range(n_pos)]
        )  # m * theta
        out.requires_grad = False  # set early to avoid an error in pytorch-1.8+
        sentinel = dim // 2 if dim % 2 == 0 else (dim // 2) + 1
        out[:, 0:sentinel] = torch.FloatTensor(np.sin(position_enc[:, 0::2]))
        out[:, sentinel:] = torch.FloatTensor(np.cos(position_enc[:, 1::2]))
        out.detach_()
        return out

    @torch.no_grad()
    def forward(self, seq_len: int, past_key_values_length: int = 0) -> Tensor:
        positions = torch.arange(
            past_key_values_length, past_key_values_length + seq_len, dtype=torch.long, device=self.weight.device
        )
        return super().forward(positions)


class Embedding(nn.Module):
    """ Class module for Roformer Embedding, word embedding & rotary positional encoding
    This module has option => whether or not to use ALBERT Style Factorized Embedding

    Args:
        cfg: configuration.py

    References:
        https://arxiv.org/abs/1706.03762
        https://arxiv.org/pdf/1810.04805.pdf
        https://arxiv.org/abs/2006.16236
        https://arxiv.org/abs/2104.09864  # RoFormer: Enhanced Transformer with Rotary Position Embedding
        https://github.com/huggingface/transformers/blob/main/src/transformers/models/roformer/modeling_roformer.py
        https://github.com/idiap/fast-transformers/blob/master/fast_transformers/attention/linear_attention.py
    """
    def __init__(self, cfg: CFG) -> None:
        super(Embedding, self).__init__()
        self.cfg = cfg
        self.batch_size = cfg.batch_size
        self.max_seq = cfg.max_seq
        self.dim_model = cfg.dim_model
        self.word_embedding = nn.Embedding(len(cfg.tokenizer), cfg.dim_model)
        self.layer_norm1 = nn.LayerNorm(cfg.dim_model, eps=cfg.layer_norm_eps)  # for word embedding
        self.hidden_dropout = nn.Dropout(p=cfg.hidden_dropout_prob)
        self.rotary_pos_encoding = RoFormerSinusoidalPositionalEmbedding(
            cfg.max_seq,
            cfg.dim_model // cfg.num_attention_heads
        )

        # ALBERT Style Factorized Embedding
        if self.cfg.is_mf_embedding:
            self.word_embedding = nn.Embedding(len(cfg.tokenizer), int(cfg.dim_model/6))
            self.projector = nn.Linear(int(cfg.dim_model/6), cfg.dim_model)  # project to original hidden dim

    def forward(self, inputs: Tensor) -> Tuple[nn.Embedding, Tensor]:
        if self.cfg.is_mf_embedding:
            word_embeddings = self.hidden_dropout(
                self.layer_norm1(self.projector(self.word_embedding(inputs)))
            )
        else:
            word_embeddings = self.hidden_dropout(
                self.layer_norm1(self.word_embedding(inputs))
            )
        rotary_pos_enc = self.rotary_pos_encoding(inputs.shape[1])
        return word_embeddings, rotary_pos_enc

🔨 Integrated RoPE into Full Attention(scaled dot-product attention)

RoPE를 적용하는 Full Attention의 구현 순서는 다음과 같다. 먼저, 단어 임베딩을 쿼리, 키, 벨류 행렬로 선형 투영한다. 이 때 RoPE를 곱해주기 위헤 apply_rotary_position_embeddings()에 인자로 쿼리, 키 행렬을 전달한다. 이 때 반드시 벨류 행렬은 단어 임베딩으로부터 선형 투영된 상태를 유지해야함을 기억하자. apply_rotary_position_embeddings()는 RoPE가 곱해진 쿼리, 키 행렬을 반환한다. 이후 과정은 퓨어한 full attention과 동일하다.

인자로 들어가는 텐서들의 모양은 주석을 참고 바란다.

def apply_rotary_position_embeddings(sinusoidal_pos: Tensor, query_layer: Tensor, key_layer: Tensor, value_layer: Tensor = None):
    """ Apply rotary position encoding to query, key layer
    Original Source code from Huggingface's RoFormer model, which is the most optimized way to create positional embedding

    You can find mathematical proof in official paper's Appendix

    Args:
        sinusoidal_pos: sinusoidal positional encoding, shape [batch(None), num_dim(None), seq_len, dim_head]
        query_layer: query matrix, shape (batch_size, num_head, seq_len, dim_head)
        key_layer: key matrix, shape (batch_size, num_head, seq_len, dim_head)
        value_layer: value matrix, shape (batch_size, num_head, seq_len, dim_head)

    References:
        https://arxiv.org/abs/2104.09864  # RoFormer: Enhanced Transformer with Rotary Position Embedding
        https://github.com/huggingface/transformers/blob/main/src/transformers/models/roformer/modeling_roformer.py#L323
    """
    sin, cos = sinusoidal_pos.chunk(2, dim=-1)  # select two element of index values
    sin_pos = torch.stack([sin, sin], dim=-1).reshape_as(sinusoidal_pos)

    cos_pos = torch.stack([cos, cos], dim=-1).reshape_as(sinusoidal_pos)
    rotate_half_query_layer = torch.stack([-query_layer[..., 1::2], query_layer[..., ::2]], dim=-1).reshape_as(
        query_layer
    )

    # mathematical expression from Appendix in official repo
    query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos
    rotate_half_key_layer = torch.stack([-key_layer[..., 1::2], key_layer[..., ::2]], dim=-1).reshape_as(key_layer)
    key_layer = key_layer * cos_pos + rotate_half_key_layer * sin_pos

    if value_layer is not None:  # In official, they don't use value_layer
        rotate_half_value_layer = torch.stack([-value_layer[..., 1::2], value_layer[..., ::2]], dim=-1).reshape_as(
            value_layer
        )
        value_layer = value_layer * cos_pos + rotate_half_value_layer * sin_pos
        return query_layer, key_layer, value_layer
    return query_layer, key_layer

class MultiHeadAttention(nn.Module):
    def __init__(
        self,
        dim_model: int = 1024,
        num_attention_heads: int = 16,
        dim_head: int = 64,
        kernel: str = 'softmax',
        attention_dropout_prob: float = 0.1
    ) -> None:
        super(MultiHeadAttention, self).__init__()
        self.dim_model = dim_model
        self.num_attention_heads = num_attention_heads
        self.dim_head = dim_head
        self.fc_q = nn.Linear(self.dim_model, self.dim_model)
        self.fc_k = nn.Linear(self.dim_model, self.dim_model)
        self.fc_v = nn.Linear(self.dim_model, self.dim_model)
        self.fc_concat = nn.Linear(self.dim_model, self.dim_model)
        self.apply_rope = apply_rotary_position_embeddings
        self.attention = scaled_dot_product_attention if kernel == 'softmax' else linear_attention
        self.attention_dropout = nn.Dropout(p=attention_dropout_prob)
        self.dot_scale = torch.sqrt(torch.tensor(self.dim_head, dtype=torch.float32))
        self.kernel = kernel
        self.eps = 1e-6
    
    def forward(self, x: Tensor, rotary_pos_enc: Tensor, padding_mask: Tensor, attention_mask: Tensor = None) -> Tensor:
        """ x is already passed nn.Layernorm, already multiplied with rotary position encoding """
        assert x.ndim == 3, f'Expected (batch, seq, hidden) got {x.shape}'

        # size: bs, seq, nums head, dim head, linear projection
        q = self.fc_q(x).reshape(-1, x.shape[1], self.num_attention_heads, self.dim_head).permute(0, 2, 1, 3).contiguous()
        k = self.fc_k(x).reshape(-1, x.shape[1], self.num_attention_heads, self.dim_head).permute(0, 2, 1, 3).contiguous()
        v = self.fc_v(x).reshape(-1, x.shape[1], self.num_attention_heads, self.dim_head).permute(0, 2, 1, 3).contiguous()

        # multiple word embedding, rotary position encoding
        rotary_q, rotary_k = self.apply_rope(rotary_pos_enc, q, k)

        attention_matrix = None
        if self.kernel == 'elu':
            attention_matrix = self.attention(
                rotary_q,
                rotary_k,
                v,
                self.kernel,
                self.eps,
                self.attention_dropout,
                padding_mask,
                attention_mask
            )
        elif self.kernel == 'softmax':  # pure self-attention
            attention_matrix = self.attention(
                rotary_q,
                rotary_k,
                v,
                self.dot_scale,
                self.attention_dropout,
                padding_mask,
                attention_mask
            )

        attention_output = self.fc_concat(attention_matrix)
        return attention_output