🌆 [ViT] An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale

🔭 Overview

시작하기 앞서, 본 논문 리뷰를 수월하게 읽으려면 Transformer 에 대한 선이해가 필수적이다. 아직 Transformer 에 대해서 잘 모른다면 필자가 작성한 포스트를 읽고 오길 권장한다. 또한 본문 내용을 작성하면서 참고한 논문과 여러 포스트의 링크를 맨 밑 하단에 첨부했으니 참고 바란다. 시간이 없으신 분들은 중간의 코드 구현부를 생략하고 Insight 부터 읽기를 권장한다.

Vision Transformer(이하 ViT)는 2020년 10월 Google에서 발표한 컴퓨터 비전용 모델이다. 자연어 처리에서 대성공을 거둔 트렌스포머 구조와 기법을 거의 그대로 비전 분야에 이식했다는 점에서 큰 의의가 있으며, 이후 컴퓨터 비전 분야의 트렌스포머 전성시대가 열리게 된 계기로 작용한다.

한편, ViT 의 설계 철학은 바로 scalability(범용성)이다. 신경망 설계에서 범용성이란, 모델의 확장 가능성을 말한다. 예를 들면 학습 데이터보다 더 크고 복잡한 데이터 세트를 사용하거나 모델의 파라미터를 늘려 사이즈를 키워도 여전히 유효한 추론 결과를 도출하거나 더 나은 성능을 보여주고 나아가 개선의 여지가 여전히 남아있을 때 “확장성이 높다” 라고 표현한다. 저자들은 논문 초반에 콕 찝어서 컴퓨터 비전 분야의 scalability 높이는 것이 이번 모델 설계의 목표였다고 밝히고 있다. 범용성은 신경망 모델 설계에서 가장 큰 화두가 되는데 도메인마다 정의하는 의미에 차이가 미세하게 존재한다. 따라서 ViT의 저자들이 말하는 범용성이 무엇을 의미하는지 알아보는 것은 구체적인 모델 구조를 이해하는데 큰 도움이 될 것이다.

🧠 Scalability in ViT

논문 초반부에서 다음과 같은 문장이 서술 되어있다.

“Our Vision Transformer (ViT) attains excellent results when pre-trained at sufficient scale and transferred to tasks with fewer datapoints"

이 구문이 ViT 의 Scalability를 가장 잘 설명하고 있다고 생각한다. 저자들이 말하는 범용성은 결국 backbone 구조의 활용을 의미한다. 자연어 처리에 익숙한 독자라면 쉽게 이해가 가능할 것이다. Transformer, GPT, BERT의 등장 이후, 자연어 처리는 범용성을 갖는 데이터 세트로 사전 훈련한 모델을 활용해 Task-Agnostic하게 하나의 backbone으로 거의 모든 Task를 수행할 수 있으며, 작은 사이즈의 데이터라도 상당히 높은 수준의 추론 성능을 낼 수 있었다. 그러나 당시 컴퓨터 비전의 메인이었던 Conv 기반 모델들은 파인튜닝해도 데이터 크기가 작으면 일반화 성능이 매우 떨어지고, Task에 따라서 다른 아키텍처를 갖는 모델을 새롭게 정의하거나 불러와 사용해야 하는 번거로움이 있었다. 예를 들면 Image Classfication 에는 ResNet, Segmentation 에는 U-Net, Object Detection 은 YOLO 를 사용하는 것처럼 말이다. 반면 자연어 처리는 사전 학습된 모델 하나로 모든 NLU, 심지어는 NLG Task도 수행할 수 있다. 저자들은 이러한 범용성을 컴퓨터 비전에도 이식 시키고 싶었던 것 같다. 그렇다면 먼저 자연어 처리에서 트랜스포머 계열이 범용성을 가질 수 있었던 이유는 무엇인지 간단히 살펴보자.

저자들은 self-attention(내적)의 효율성, 모델의 구조적 탁월성 그리고 self-supervised task의 존재를 꼽는다. 그럼 이것들이 왜 범용성을 높이는데 도움이 될까??

self-attention(내적)은 행렬 간 곱셉으로 정의 되어 설계가 매우 간편하고 병렬로 한번에 처리하는 것이 가능하기 때문에 효율적으로 전체 데이터를 모두 고려한 연산 결과를 얻을 수 있다.

Multi-Head Attention 구조는 여러 차원의 의미 관계를 동시에 포착하고 그것을 앙상블한 것과 같은(실제로는 MLP) 결과를 얻을 수 있다는 점에서 구조적으로 탁월하다.

마지막으로 MLM, Auto-Regression(LM) Task는 데이터 세트에 별도의 인간의 개입(라벨링)이 필요하지 않기 때문에 가성비 있게 데이터와 모델의 사이즈를 늘릴 수 있게 된다.
이제 논문에서 트랜스포머 계열이 가진 범용성을 어떻게 비전 분야에 적용했는지 주목하면서 모델 구조를 하나 하나 살펴보자.

🌟 Modeling

ViT Model Structure

• 1) Transfer Scalability from pure Transformer to Computer Vision
  • Overcome reliance on Convolution(Inductive Bias) in Computer Vision
  • Apply Self-Attention & Architecture from vanilla NLP Transformers as closely as possible
  • Treat Image as sequence of text token
  • Make $P$ sub-patches from whole image, playing same role as token in NLP Transformer

저자들은 먼저 Conv 에 대한 의존을 버릴 것을 주장한다. Conv가 가진 Inductive Bias 때문에 파인튜닝 레벨에서 데이터 크기가 작으면 일반화 성능이 떨어지는 것이라고 설명하고 있다. 이 말을 이해하려면 Inductive Bias에 대해서 먼저 알아야 한다. Inductive Bias란, 주어진 데이터로부터 일반화 성능을 높이기 위해 ‘입력되는 데이터는 ~ 할 것이다’, ‘이런 특징을 갖고 있을 것이다’와 같은 가정, 가중치, 가설 등을 기계학습 알고리즘에 적용하는 것을 말한다.

Conv 연산 자체 (가중치 공유, 풀링 있는 Conv Block이 Invariance)의 기본 가정은 translation equivariance, locality이다. 사실 저자의 주장을 이해하는데 equivariance와 locality의 뜻이 무엇인지 파악하는 것은 크게 의미가 없다 (equivariance와 invariance에 대해서는 다른 포스팅에서 자세히 살펴보도록 하겠다). 중요한 것은 입력 데이터에 가정을 더한다는 점이다. 만약 주어진 입력이 미리 가정한 Inductive Bias 에 벗어난다면 어떻게 될까??

아마 오버피팅 되거나 모델 학습이 수렴성을 갖지 못하게 될 것이다. 이미지 데이터도 Task에 따라 필요한 Inductive Bias가 달라진다. 예를 들어 Segmentation, Detection 의 경우는 이미지 속 객체의 위치, 픽셀 사이의 spatial variance 정보가 매우 중요하다. 한편, Classification은 spatial invariance가 중요하다. 목표 객체의 위치와 주변 특징보다 타겟 자체를 신경망이 인식하는 것이 중요하기 때문이다. 따라서 ViT 저자들은 어떤 Bias던 상관없이 편향을 갖고 데이터를 본다는 것 자체에 의문을 표하며, 이미지 역시 Inductive Bias에서 벗어나, 주어진 데이터 전체 특징(패치) 사이의 관계를 파악하는 과정에서 scalability를 획득할 수 있다고 주장한다.

그래서 Conv의 대안으로 상대적으로 Inductive Bias 가 부족한 Self-Attention, Transformer Architecture를 사용한다. 두가지의 효용성에 대해서는 이미 위에서 언급했기 때문에 생략하고, 여기서 짚고 넘어가야할 점은 Self-Attention이 Conv 대비 Inductive Bias가 적다는 점이다. Self-Attention 과정에는 여러 연산, 스케일 조정값들이 포함되지만 본질적으로 “내적” 이 중심이다. 내적은 그 어떤 편향 (Conv와 대조하려고 이렇게 서술했지만 사실 Position Embedding 더하는 것도 일종의 약한 Inductive Bias)이 존재하지 않는다. 일단 주어진 모든 데이터에 대해서 내적값을 산출하고 그 다음에 관계가 있다고 생각되는 정보를 추리기 때문이다. Conv 때와 달리 ‘입력되는 데이터는 ~ 할 것이다’, ‘이런 특징을 갖고 있을 것이다’ 라는 가정이 없다. 이번 포스팅의 마지막 쯤에서 다시 다루겠지만 그래서 ViT는 인스턴스 사이의 모든 관계를 뽑아보는 Self-Attention(내적) 을 기반으로 만들어졌기 때문에 이미지의 Global Information을 포착하는데 탁월한 성능을 보이고, Conv 는 “중요한 정보는 근처 픽셀에 몰려있다라는” Inductive Bias 덕분에 Local Information을 포착하는데 탁월한 성능을 낸다.

그렇다면 픽셀 하나 하나끼리 내적해준다는 것일까?? 아니다 여기서 논문의 제목이 An Image Is Worth 16x16 Words 인 이유가 드러난다. 일단 픽셀 하나 하나끼리 유사도를 측정하는 것이 유의미할까 생각해보자. 자연어의 토큰과 달리 이미지의 단일 픽셀 한 개는 큰 인사이트를 얻기 힘들다. 픽셀은 말 그대로 점 하나일 뿐이다. 픽셀을 여러 개 묶어 패치 단위로 묶는다면 이야기는 달라진다. 일정 크기 이상의 패치라면 자연어의 토큰처럼 그 자체로 어떤 의미를 담을 수 있다. 따라서 저자는 전체 이미지를 여러 개의 16x16 혹은 14x14 사이즈 패치로 나누어 하나 하나를 토큰으로 간주해 이미지 시퀀스를 만들고 그것을 모델의 Input으로 사용한다.

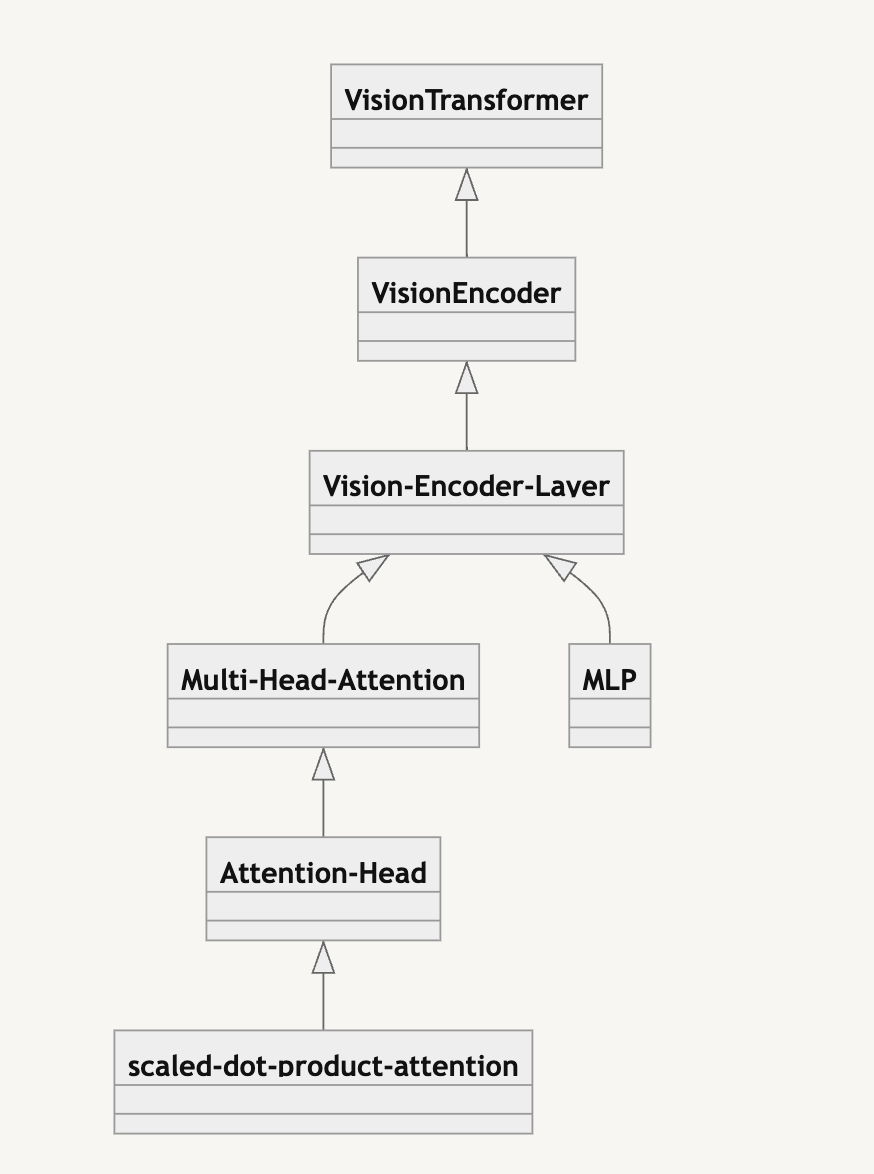Class Diagram

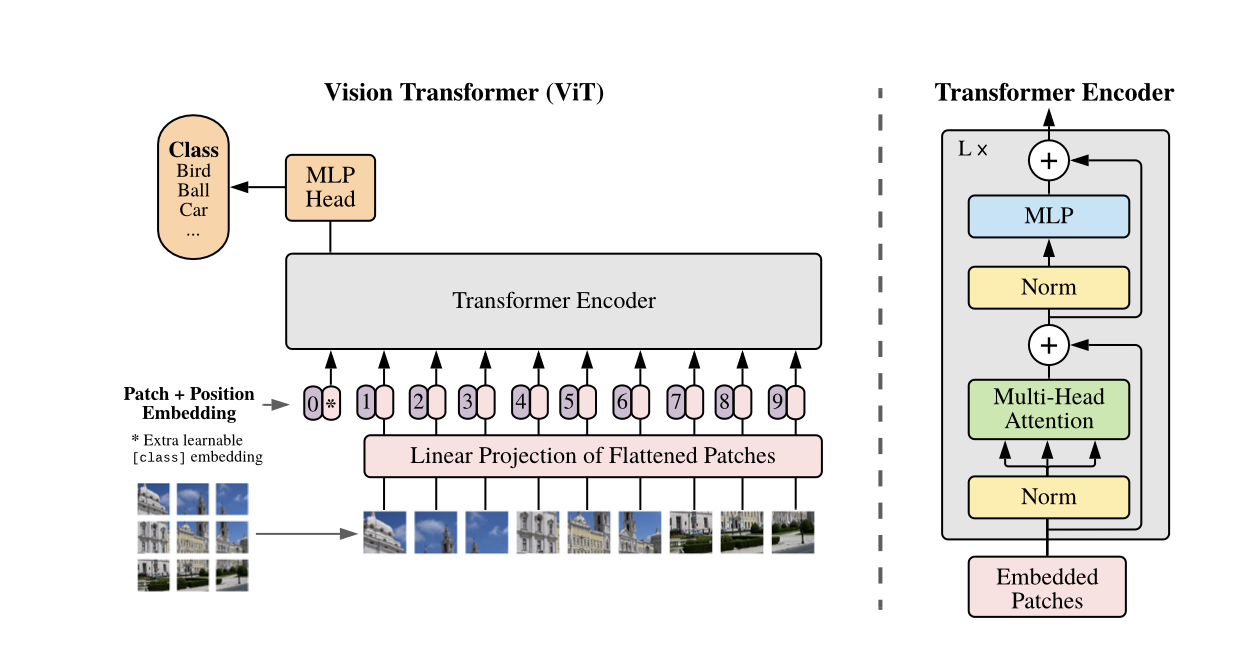
모델 구조의 뼈대가 되는 내용들을 모두 살펴보았고, 위에서 서술한 내용을 구현하기 위해 어떤 블록들을 사용했는지 필자가 직접 논문을 보고 따라 구현한 코드와 함께 알아보도록 하자. 위에 첨부한 모델 모식도에 나와 있는 블록들 하나 하나 살펴볼 예정이다. 여담으로 Google Research의 Official Repo 역시 함께 참고했는데, 코드가 모두 구글이 요새 새롭게 미는 Jax, Flax 로 구현 되어 있었다. 파이토치나 좀 써본 필자 입장에서는 정말 … 지옥불을 경험했다. 오늘도 다시 한 번 페이스북 파이토치 개발팀에 큰절 드리고 싶다.

🔬 Linear Projection of Flattened Patches

\[x_p \in R^{N * (P^2•C)}\] \[z_{0} = [x_{class}; x_p^1E;x_p^2E;x_p^3E....x_p^NE]\] \[N = \frac{H*W}{P*P}\]

ViT의 입력 임베딩을 생성하는 역할을 한다. ViT는 $x \in R^{H * W * C}$(H: height, W: width, C: channel)의 형상을 갖는 이미지를 입력으로 받아 가로 세로 길이가 $P$, 채널 개수 $C$인 $N$개의 패치로 reshape 한다. 필자가 코드 구현 중 가장 혼동한 부분이 바로 패치 개수 $N$이었다. 직관적으로 패치 개수라고 하면, 전체 이미지 사이즈에서 패치 크기를 나눈 값이라고 생각하기 쉽기 때문이다. 예를 들면 512x512짜리 이미지를 16x16 사이즈의 패치로 나눈다고 해보자. 필자는 단순히 512/16=32 라는 결과를 이용해 $N=32$로 설정하고 실험을 진행하다가 텐서 차원이 맞지 않아 발생하는 에러 로그를 마주했었다. 그러나 논문 속 수식을 확인해보면, $H * W / P^2$이 바로 패치 개수$N$으로 정의된다. 그래서 만약 512x512 사이즈의 RGB 이미지 10장을 ViT 입력 임베딩에 맞게 차원 변환한다면 결과는 [10, 3, 1024, 768] 이 될 것이다. (이 예시를 앞으로 계속 이용하겠다)

이렇게 차원을 바꿔준 이미지를 nn.Linear((channels * patch_size**2), dim_model) 를 통해 ViT의 임베딩 레이어에 선형 투영해준다. 여기서 자연어 처리와 파이토치를 자주 사용하시는 독자라면 왜 nn.Embedding을 사용하지 않았는가 의문을 가질 수 있다.

자연어 처리에서 입력 임베딩을 만들때는 모델의 토크나이저에 의해 사전 정의된 vocab의 사이즈가 입력 문장에 속한 토큰 개수보다 훨씬 크기 때문에 데이터 룩업 테이블 방식의 nn.Embedding 을 사용하게 된다. 이게 무슨 말이냐면, 토크나이저에 의해 사전에 정의된 vocab 전체가 nn.Embedding(vocab_size, dim_model)로 투영 되어 가로는 vocab 사이즈, 세로는 모델의 차원 크기에 해당하는 룩업 테이블이 생성되고, 내가 입력한 토큰들은 전체 vocab의 일부분일테니 전체 임베딩 룩업 테이블에서 내가 임베딩하고 싶은 토큰들의 인덱스만 알아낸다는 것이다.

그래서 nn.Embedding 에 정의된 차원과 실제 입력 데이터의 차원이 맞지 않아도 함수가 동작하게 되는 것이다. 그러나 비전의 경우, 사전에 정의된 vocab이라는 개념이 전혀 없고 입력 이미지 역시 항상 고정된 크기의 차원으로 들어오기 때문에 nn.Embedding이 아닌 nn.Linear 을 사용해 곧바로 선형 투영을 구현한 것이다. 두 메서드에 대한 자세한 비교는 파이토치 관련 포스트에서 다시 한 번 자세히 다루도록 하겠다.

한편, Position Embedding을 더하기 전, Input Embedding의 차원은 [10, 1024, 1024] 이 된다. 지금까지 설명한 부분(Linear Projection of Flattened Patches )을 파이토치 코드로 구현하면 다음과 같다.

class VisionTransformer(nn.Module):
    ...
    중략
    ...
    self.num_patches = int(image_size / patch_size)**2
    self.input_embedding = nn.Linear((channels * patch_size**2), dim_model) # Projection Layer for Input Embedding
    ...
    중략
    ...  
    def forward(self, inputs: Tensor) -> any:
        """ For cls pooling """
        assert inputs.ndim != 4, f"Input shape should be [BS, CHANNEL, IMAGE_SIZE, IMAGE_SIZE], but got {inputs.shape}"
        x = inputs 
        x = self.input_embedding(
            x.reshape(x.shape[0], self.num_patches, (self.patch_size**2 * x.shape[1])) # Projection Layer for Input Embedding
        )
        cls_token = torch.zeros(x.shape[0], 1, x.shape[2])  # can change init method
        x = torch.cat([cls_token, x], dim=1)
    ...

임베딩 레이어를 객체로 따로 구현해도 되지만, 필자는 굳이 추상화가 필요하지 않다고 생각해 ViT의 최상위 클래스인 VisionTransformer의 forward 메서드 맨 초반부에 구현하게 되었다. 입력 받은 이미지 텐서를 torch.reshape 을 통해 [패치 개수, 픽셀개수*채널개수] 로 바꾼 뒤, 미리 정의해둔 self.input_embedding 에 매개변수로 전달해 “위치 임베딩” 값이 더해지기 전 Input Embedding을 만든다.

한편, CLS Pooling을 위해 마지막에 [batch, 1, image_size] 의 차원을 갖는 cls_token 을 정의해 패치 시퀀스와 concat (맨 앞에)해준다. 이 때 논문에 제시된 수식 상, CLS Token은 선형 투영하지 않으며, 패치 시퀀스에 선형 투영이 이뤄지고 난 뒤에 맨 앞에 Concat 하게 된다.

CLS Token까지 더한 최종 Input Embedding 의 텐서 차원은 [10, 1025, 1024] 가 된다.

🔢 Positional Embedding

\[E_{pos} \in R^{(N+1)*D}\]

이미지를 패치 단위의 임베딩으로 만들었다면 이제 위치 임베딩을 정의해서 더해주면 모식도 속 Embedded Patches , 즉 인코더에 들어갈 최종 Patch Embedding 이 완성 된다. 위치 임베딩을 만드는 방식은 기존 Transformer, BERT 와 동일하다. 아래 VisionEncoder 클래스를 구현한 코드를 살펴보자.

 class VisionEncoder(nn.Module):
    ...
    중략
    ...
    self.positional_embedding = nn.Embedding((self.num_patches + 1), dim_model)  # add 1 for cls token
    ...
    중략
    ...
    def forward(self, inputs: Tensor) -> tuple[Tensor, Tensor]:
        layer_output = []
        pos_x = torch.arange(self.num_patches + 1).repeat(inputs.shape[0]).to(inputs)  # inputs.shape[0] = Batch Size of Input
        x = self.dropout(
            inputs + self.positional_embedding(pos_x)
        )
    ...

Input Embedding과 다르게 위치 임베딩은 nn.Embedding으로 구현했는데, 여기서도 사실 nn.Linear를 사용해도 무방하다. 그것보다 nn.Embedding의 입력 차원인 self.num_patches + 1 에 주목해보자. 왜 1을 더해준 값을 사용했을까??

ViT는 BERT의 CLS Token Pooling 을 차용하기 위해 패치 시퀀스 맨 앞에 CLS 토큰을 추가하기 때문이다. 이렇게 추가된 CLS Token은 인코더를 거쳐 최종 MLP Head에 흘러들어가 로짓으로 변환된다. 만약 독자께서 CLS Token Pooling 대신 다른 풀링 방식을 사용할거라면 1을 추가해줄 필요는 없다.

애초에 객체 인스턴스 초기화 당시에 CLS Token 을 추가를 반영한 값을 전달하면 되지 않는가하는 의문이 들 수도 있다. 하지만 VisionEncoder 객체 인스턴스 초기화 당시에는 num_patches 값으로 CLS Token이 추가되기 이전 값(+1 반영이 안되어 있음)을 전달하도록 설계 되어 있어서 CLS Pooling을 사용할거라면 1 추가를 꼭 해줘야 한다.

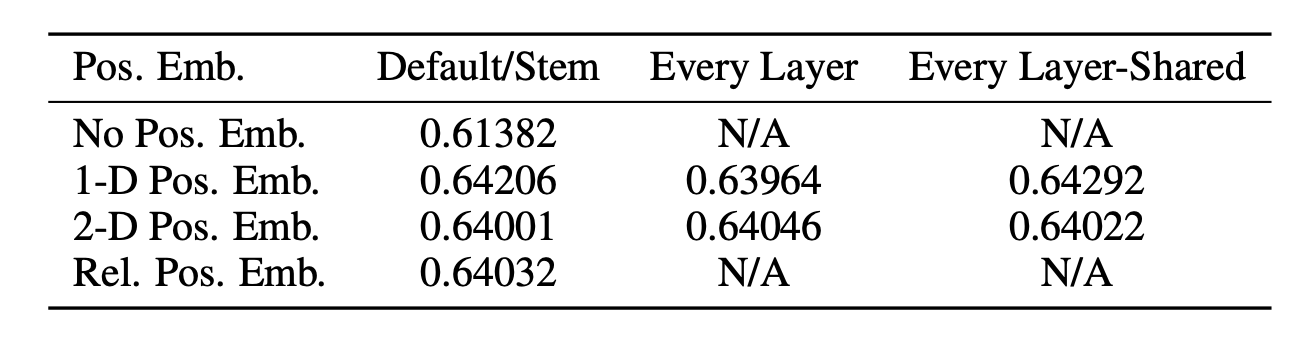Performance Table by making Position Embedding method

한편 저자는 2D Postion Embedding, Relative Position Embedding 방식도 적용해봤지만, 구현 복잡도 & 연산량 대비 성능 향상 폭이 매우 미미해 일반적인 1D Position Embedding을 사용할 것을 추천하고 있다.

👩‍👩‍👧‍👦 Multi-Head Attention

\[z_t^{'} = MSA(LN(z_{t-1}) + z_{t-1})\] \[MSA(z) = [SA_1();SA_2();SA_3()...SA_k()]*U_{msa}, \ \ U_{msa} \in R^{(k*D_h)*D} \\\]

트랜스포머 계열 모델의 핵심 Multi-Head Self-Attention 모듈에 대해서 알아보자. 사실 기존 자연어 처리 Transformer, BERT 등의 동작 방식과 완전히 동일하며, 코드로 구현할 때 역시 동일하게 만들어주면 된다. 자세한 원리와 동작 방식은 Attention Is All You Need 리뷰 포스트에서 설명했기 때문에 생략하고 넘어가겠다. 한편 파이토치로 구현한 Multi-Head Self-Attention 블럭에 대한 코드는 다음과 같다.

def scaled_dot_product_attention(q: Tensor, k: Tensor, v: Tensor, dot_scale: Tensor) -> Tensor:
    """
    Scaled Dot-Product Attention
    Args:
        q: query matrix, shape (batch_size, seq_len, dim_head)
        k: key matrix, shape (batch_size, seq_len, dim_head)
        v: value matrix, shape (batch_size, seq_len, dim_head)
        dot_scale: scale factor for Q•K^T result, same as pure transformer
    Math:
        A = softmax(q•k^t/sqrt(D_h)), SA(z) = Av
    """
    attention_dist = F.softmax(
        torch.matmul(q, k.transpose(-1, -2)) / dot_scale,
        dim=-1
    )
    attention_matrix = torch.matmul(attention_dist, v)
    return attention_matrix

class AttentionHead(nn.Module):
    """
    In this class, we implement workflow of single attention head
    Args:
        dim_model: dimension of model's latent vector space, default 1024 from official paper
        dim_head: dimension of each attention head, default 64 from official paper (1024 / 16)
        dropout: dropout rate, default 0.1
    Math:
        [q,k,v]=z•U_qkv, A = softmax(q•k^t/sqrt(D_h)), SA(z) = Av
    """
    def __init__(self, dim_model: int =  1024, dim_head: int = 64, dropout: float = 0.1) -> None:
        super(AttentionHead, self).__init__()
        self.dim_model = dim_model
        self.dim_head = dim_head
        self.dropout = dropout
        self.dot_scale = torch.sqrt(torch.tensor(self.dim_head))
        self.fc_q = nn.Linear(self.dim_model, self.dim_head)
        self.fc_k = nn.Linear(self.dim_model, self.dim_head)
        self.fc_v = nn.Linear(self.dim_model, self.dim_head)

    def forward(self, x: Tensor) -> Tensor:
        attention_matrix = scaled_dot_product_attention(
            self.fc_q(x),
            self.fc_k(x),
            self.fc_v(x),
            self.dot_scale
        )
        return attention_matrix

class MultiHeadAttention(nn.Module):
    """
    In this class, we implement workflow of Multi-Head Self-Attention
    Args:
        dim_model: dimension of model's latent vector space, default 1024 from official paper
        num_heads: number of heads in MHSA, default 16 from official paper for ViT-Large
        dim_head: dimension of each attention head, default 64 from official paper (1024 / 16)
        dropout: dropout rate, default 0.1
    Math:
        MSA(z) = [SA1(z); SA2(z); · · · ; SAk(z)]•Umsa
    Reference:
        https://arxiv.org/abs/2010.11929
        https://arxiv.org/abs/1706.03762
    """
    def __init__(self, dim_model: int = 1024, num_heads: int = 8, dim_head: int = 64, dropout: float = 0.1) -> None:
        super(MultiHeadAttention, self).__init__()
        self.dim_model = dim_model
        self.num_heads = num_heads
        self.dim_head = dim_head
        self.dropout = dropout
        self.attention_heads = nn.ModuleList(
            [AttentionHead(self.dim_model, self.dim_head, self.dropout) for _ in range(self.num_heads)]
        )
        self.fc_concat = nn.Linear(self.dim_model, self.dim_model)

    def forward(self, x: Tensor) -> Tensor:
        """ x is already passed nn.Layernorm """
        assert x.ndim == 3, f'Expected (batch, seq, hidden) got {x.shape}'
        attention_output = self.fc_concat(
            torch.cat([head(x) for head in self.attention_heads], dim=-1)  # concat all dim_head = num_heads * dim_head
        )
        return attention_output

MultiHeadAttention을 가장 최상위 객체로 두고, 하위에 AttentionHead객체를 따로 구현했다. 이렇게 구현하면, 어텐션 해드별로 쿼리, 키, 벨류 선영 투영 행렬(nn.Linear)을 따로 구현해줄 필요가 없어지며, nn.ModuleList 를 통해 개별 해드를 한 번에 그룹핑하고 loop 를 통해 출력 결과를 concat 해줄 수 있어 복잡하고 많은 에러를 유발하는 텐서 차원 조작을 피할 수 있으며, 코드의 가독성이 올라가는 효과가 있다.

🗳️ MLP

\[z_{t} = MLP(LN(z_{t}^{'}) + z_{t}^{'})\]

이름만 MLP로 바뀌었을 뿐, 기존 트랜스포머의 피드 포워드 블럭과 동일한 역할을 한다. 역시 자세한 동작 방식은 여기 포스트에서 확인하자. 파이토치로 구현한 코드는 다음과 같다.

class MLP(nn.Module):
    """
    Class for MLP module in ViT-Large
    Args:
        dim_model: dimension of model's latent vector space, default 512
        dim_mlp: dimension of FFN's hidden layer, default 2048 from official paper
        dropout: dropout rate, default 0.1
    Math:
        MLP(x) = MLP(LN(x))+x
    """
    def __init__(self, dim_model: int = 1024, dim_mlp: int = 4096, dropout: float = 0.1) -> None:
        super(MLP, self).__init__()
        self.mlp = nn.Sequential(
            nn.Linear(dim_model, dim_mlp),
            nn.GELU(),
            nn.Dropout(p=dropout),
            nn.Linear(dim_mlp, dim_model),
            nn.Dropout(p=dropout),
        )

    def forward(self, x: Tensor) -> Tensor:
        return self.mlp(x)

특이한 점은 Activation Function으로 GELU를 사용(기존 트랜스포머는 RELU)했다는 점이다.

📘 Vision Encoder Layer

ViT 인코더 블럭 1개에 해당하는 하위 모듈과 동작을 구현한 객체이다. 구현한 코드는 아래와 같다.

class VisionEncoderLayer(nn.Module):
    """
    Class for encoder_model module in ViT-Large
    In this class, we stack each encoder_model module (Multi-Head Attention, Residual-Connection, Layer Normalization, MLP)
    """
    def __init__(self, dim_model: int = 1024, num_heads: int = 16, dim_mlp: int = 4096, dropout: float = 0.1) -> None:
        super(VisionEncoderLayer, self).__init__()
        self.self_attention = MultiHeadAttention(
            dim_model,
            num_heads,
            int(dim_model / num_heads),
            dropout,
        )
        self.layer_norm1 = nn.LayerNorm(dim_model)
        self.layer_norm2 = nn.LayerNorm(dim_model)
        self.dropout = nn.Dropout(p=dropout)
        self.mlp = MLP(
            dim_model,
            dim_mlp,
            dropout,
        )

    def forward(self, x: Tensor) -> Tensor:
        ln_x = self.layer_norm1(x)
        residual_x = self.dropout(self.self_attention(ln_x)) + x

        ln_x = self.layer_norm2(residual_x)
        fx = self.mlp(ln_x) + residual_x  # from official paper & code by Google Research
        return fx

특이점은 마지막 MLP Layer와 Residual 결과를 더한 뒤, 다음 인코더 블록에 전달하기 전에 층 정규화를 한 번 더 적용한다는 것이다. 모델 모식도에는 나와 있지 않지만, 본문에 해당 내용이 실려 있다. 마지막 인코더의 출력값에만 한번 더 layernorm을 적용한다.

📚 VisionEncoder

입력 이미지를 Patch Embedding으로 인코딩 하고 N개의 VisionEncoderLayer를 쌓기 위해 구현된 객체이다. Patch Embedding을 만드는 부분은 이미 위에서 설명했기 때문에 넘어가고, 인코더 블럭을 N개 쌓는 방법은 역시나 nn.ModuleList 를 사용하면 간편하게 구현할 수 있다. 아래 코드를 살펴보자.

class VisionEncoder(nn.Module):
    """
    In this class, encode input sequence(Image) and then we stack N VisionEncoderLayer
    This model is implemented by cls pooling method for classification
    First, we define "positional embedding" and then add to input embedding for making patch embedding
    Second, forward patch embedding to N EncoderLayer and then get output embedding
    Args:
        num_patches: number of patches in input image => (image_size / patch_size)**2
        N: number of EncoderLayer, default 24 for large model
    """

    def __init__(self, num_patches: int, N: int = 24, dim_model: int = 1024, num_heads: int = 16, dim_mlp: int = 4096, dropout: float = 0.1) -> None:
        super(VisionEncoder, self).__init__()
        self.num_patches = num_patches
        self.positional_embedding = nn.Embedding((self.num_patches + 1), dim_model)  # add 1 for cls token
        self.num_layers = N
        self.dim_model = dim_model
        self.num_heads = num_heads
        self.dim_mlp = dim_mlp
        self.dropout = nn.Dropout(p=dropout)
        self.encoder_layers = nn.ModuleList(
            [VisionEncoderLayer(dim_model, num_heads, dim_mlp, dropout) for _ in range(self.num_layers)]
        )
        self.layer_norm = nn.LayerNorm(dim_model)

    def forward(self, inputs: Tensor) -> tuple[Tensor, Tensor]:
        layer_output = []
        pos_x = torch.arange(self.num_patches + 1).repeat(inputs.shape[0]).to(inputs)
        x = self.dropout(
            inputs + self.positional_embedding(pos_x)
        )
        for layer in self.encoder_layers:
            x = layer(x)
            layer_output.append(x)
        encoded_x = self.layer_norm(x)  # from official paper & code by Google Research
        layer_output = torch.stack(layer_output, dim=0).to(x.device)  # For Weighted Layer Pool: [N, BS, SEQ_LEN, DIM]
        return encoded_x, layer_output

마지막 층의 인코더 출력값에는 layernorm을 적용해줘야 함을 잊지 말자. 한편, layer_output는 레이어 별 어텐션 결과를 시각화 하거나 나중에 WeightedLayerPool에 사용하려고 만들었다.

🤖 VisionTransformer

ViT Model Variant

ViT 모델의 가장 최상위 객체로, 앞에서 설명한 모든 모듈들의 동작이 이뤄지는 곳이다. 사용자로부터 하이퍼파라미터를 입력 받아 모델의 크기, 깊이, 패치 크기, 이미지 임베딩 추출 방식을 지정한다. 그리고 입력 이미지를 전달받아 임베딩을 만들고 인코더에 전달한 뒤, MLP Head 를 통해 최종 예측 결과를 반환하는 역할을 한다.

이미지 임베딩 추출 방식은 Linear Projection과 Convolution이 있다. 전자가 논문에서 말하는 일반적인 ViT를 말하며 후자는 저자가 Hybrid ViT라고 따로 명명하는 모델이다. 임베딩 추출 방식 이외에 다른 차이는 전혀 없다. extractor 매개변수를 통해 임베딩 추출 방식을 지정할 수 있으니 아래 코드를 확인해보자.

class VisionTransformer(nn.Module):
    """
    Main class for ViT of cls pooling, Pytorch implementation
    We implement pure ViT, Not hybrid version which is using CNN for extracting patch embedding
    input must be [BS, CHANNEL, IMAGE_SIZE, IMAGE_SIZE]
    In NLP, input_sequence is always smaller than vocab size
    But in vision, input_sequence is always same as image size, not concept of vocab in vision
    So, ViT use nn.Linear instead of nn.Embedding for input_embedding
    Args:
        num_classes: number of classes for classification task
        image_size: size of input image, default 512
        patch_size: size of patch, default 16 from official paper for ViT-Large
        extractor: option for feature extractor, default 'base' which is crop & just flatten
                   if you want to use Convolution for feature extractor, set extractor='cnn' named hybrid ver in paper
        classifier: option for pooling method, default token meaning that do cls pooling
                    if you want to use mean pooling, set classifier='mean'
        mode: option for train type, default fine-tune, if you want pretrain, set mode='pretrain'
              In official paper & code by Google Research, they use different classifier head for pretrain, fine-tune
    Math:
        image2sequence: [batch, channel, image_size, image_size] -> [batch, patch, patch_size^2*channel]
        input_embedding: R^(P^2 ·C)×D
    Reference:
        https://arxiv.org/abs/2010.11929
        https://arxiv.org/abs/1706.03762
        https://github.com/google-research/vision_transformer/blob/main/vit_jax/models_vit.py#L184
    """
    def __init__(
            self,
            num_classes: int,
            channels: int = 3,
            image_size: int = 512,
            patch_size: int = 16,
            num_layers: int = 24,
            dim_model: int = 1024,
            num_heads: int = 16,
            dim_mlp: int = 4096,
            dropout: float = 0.1,
            extractor: str = 'base',
            classifier: str = 'token',
            mode: str = 'fine_tune',
    ) -> None:
        super(VisionTransformer, self).__init__()
        self.num_patches = int(image_size / patch_size)**2
        self.num_layers = num_layers
        self.patch_size = patch_size
        self.dim_model = dim_model
        self.num_heads = num_heads
        self.dim_mlp = dim_mlp
        self.dropout = nn.Dropout(p=dropout)

        # Input Embedding
        self.extractor = extractor
        self.input_embedding = nn.Linear((channels * patch_size**2), dim_model)
        self.conv = nn.Conv2d(
            in_channels=channels,
            out_channels=self.dim_model,
            kernel_size=self.patch_size,
            stride=self.patch_size
        )

        # Encoder Multi-Head Self-Attention
        self.encoder = VisionEncoder(
            self.num_patches,
            self.num_layers,
            self.dim_model,
            self.num_heads,
            self.dim_mlp,
            dropout,
        )
        self.classifier = classifier
        self.pretrain_classifier = nn.Sequential(
            nn.Linear(self.dim_model, self.dim_model),
            nn.Tanh(),
        )
        self.fine_tune_classifier = nn.Linear(self.dim_model, num_classes)
        self.mode = mode

    def forward(self, inputs: Tensor) -> any:
        """ For cls pooling """
        assert inputs.ndim != 4, f"Input shape should be [BS, CHANNEL, IMAGE_SIZE, IMAGE_SIZE], but got {inputs.shape}"
        x = inputs

        if self.extractor == 'cnn':
            # self.conv(x).shape == [batch, dim, image_size/patch_size, image_size/patch_size]
            x = self.conv(x).reshape(x.shape[0], self.dim_model, self.num_patches**2).transpose(-1, -2)
        else:
            # self.extractor == 'base':
            x = self.input_embedding(
                x.reshape(x.shape[0], self.num_patches, (self.patch_size**2 * x.shape[1]))
            )
        cls_token = torch.zeros(x.shape[0], 1, x.shape[2])  # can change init method
        x = torch.cat([cls_token, x], dim=1)

        x, layer_output = self.encoder(x)  # output

        # classification
        x = x[:, 0, :]  # select cls token, which is position 0 in sequence
        if self.mode == 'fine_tune':
            x = self.fine_tune_classifier(x)

        if self.mode == 'pretrain':
            x = self.fine_tune_classifier(self.pretrain_classifier(x))
        return x

한편, 코드에서 눈여겨봐야 할 점은 MLP Head로, 저자는 pre-train 시점과 fine-tune 시점에 서로 다른 Classifier Head를 사용한다. 전자에는 Activation Function 1개와 두 개의 MLP Layer를 사용하고, 후자에는 1개의 MLP Layer를 사용한다.

다만, pretrain_classifier의 입출력 차원에 대한 정확한 수치를 논문이나 official repo code를 확인해도 찾을 수 없었다, 그래서 임시로 모델의 차원과 똑같이 세팅하게 되었다.

또한 저자는 CLS Pooling과 더불어 GAP 방식도 제시하는데, GAP 방식은 추후에 따로 추가가 필요하다. 그리고 사전 훈련과 파인 튜닝 모두 분류 테스크를 수행했는데 (심지어 같은 데이터 세트를 사용함) 왜 굳이 서로 다른 Classifier Head를 정의했는지 의도를 알 수 없어 논문을 다시 읽어봤지만, 이유에 대해서 상세히 언급하는 부분이 없었다.

ViT는 입력 임베딩을 정의하는 부분을 제외하면 저자의 의도대로 기존 트랜스포머와 동일한 모델 구조를 가졌다. 완전히 다른 데이터인 이미지와 텍스트에 같은 구조의 모델을 적용한다는 것이 정말 쉽지 않아 보였는데, 패치 개념을 만들어 자연어의 토큰처럼 간주하고 사용한 것이 의도대로 구현하는데 직관적이면서도 정말 효과적이었다고 생각한다. 이제 이렇게 만들어진 모델을 통해 진행한 여러 실험 결과에 어떤 인사이트가 담겨 있는지 알아보자.

🔬 Insight from Experiment

💡 Insight 1. ViT의 Scalability 증명

• Pre-Train에 사용되는 이미지 데이터 세트의 크기가 커질수록 Fine-Tune Stage에서 ViT가 CNN보다 높은 성능
• 같은 성능이라면 ViT가 상대적으로 적은 연산량을 기록

Performance per Dataset Scale

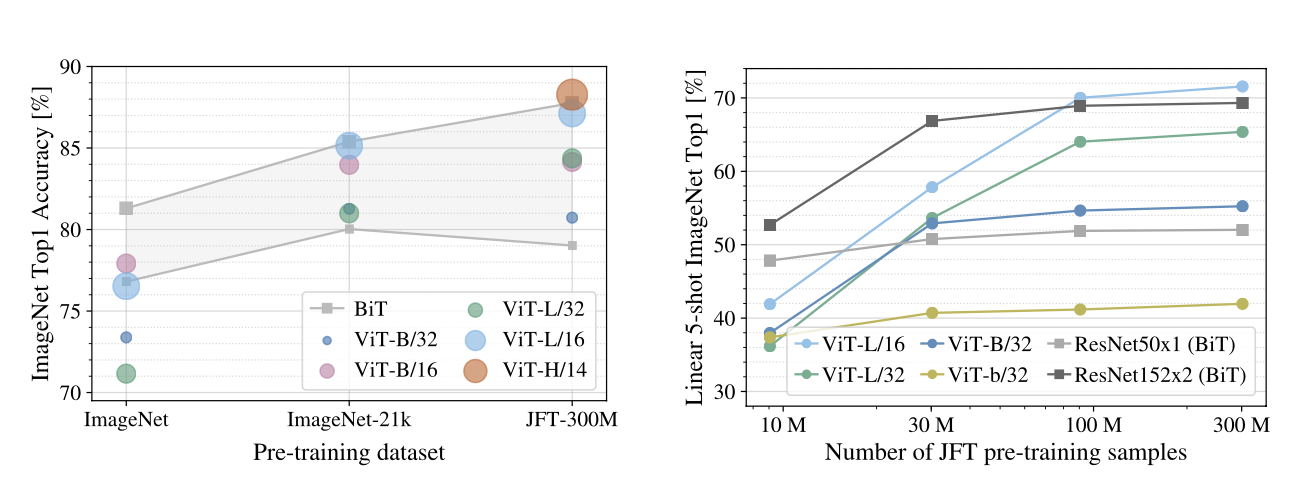
위 도표는 Pre-Train Stage에 사용된 이미지 데이터 세트에 따른 모델의 Fine-Tune 성능 추이를 나타낸 자료다. 사전 훈련 데이터 스케일이 크지 않을 때는 Conv 기반의 ResNet 시리즈가 ViT 시리즈를 압도하는 모습을 보여준다. 하지만 데이터 세트의 크기가 커질수록 점점 ViT 시리즈의 성능이 ResNet을 능가하는 결과를 볼 수 있다.

한편, ViT & ResNet 성능 결과 모두 ImageNet과 JFT-Image로 사전 훈련 및 파인 튜닝을 거쳐 나왔다고 하니 참고하자. 추가로 파인 튜닝 과정에서 사전 훈련 때보다 이미지 사이즈를 키워서 훈련을 시켰다고 논문에서 밝히고 있는데, 이는 저자의 실험 결과에 기인한 것이다. 논문에 따르면 파인 튜닝 때 사전 훈련 당시보다 더 높은 해상도의 이미지를 사용하면 성능이 향상 된다고 하니 기억했다가 써먹어보자.

Performance per FLOPs

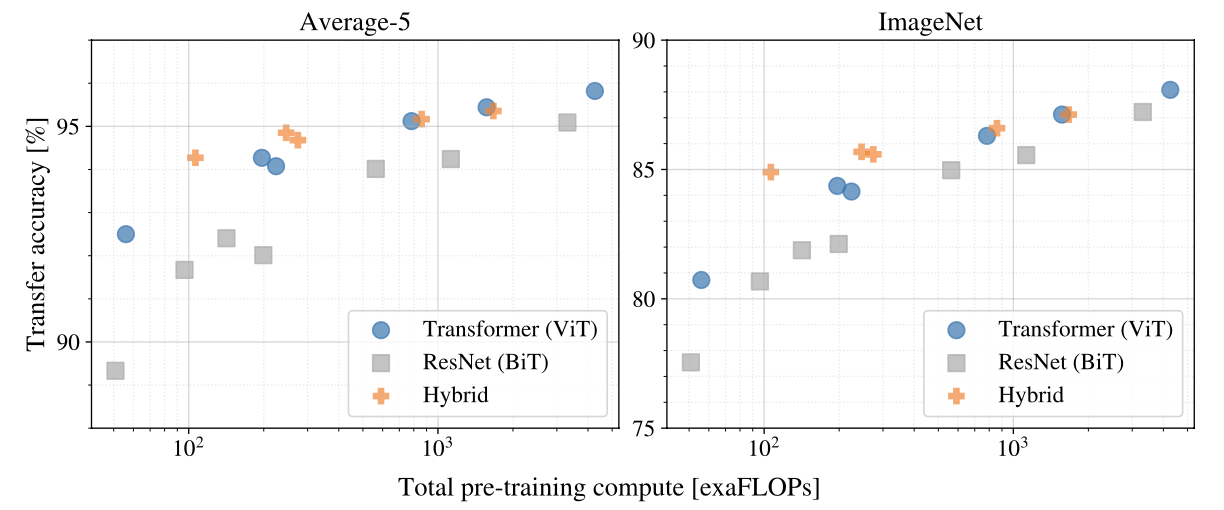
위 도표는 연산량 변화에 따른 모델의 성능 추이를 나타낸 그림이다. 두 지표 모두 같은 점수라면 ViT 시리즈의 연산량이 현저히 적음을 알 수 있다. 또한 정확도 95% 이하 구간에서 같은 성능이라면 ViT의 Hybrid 버전 모델의 연산량이 일반 ViT 버전보다 현저히 적음을 확인할 수 있다. 이러한 사실은 추후에 Swin-Transformer 설계에 영감을 준다.

두 개의 실험 결과를 종합했을 때, ViT가 ResNet보다 일반화 성능이 더 높으며(도표 1) 모델의 Saturation 현상이 두드러지지 않아 성능의 한계치(도표 2) 역시 더 높다고 볼 수 있다. 따라서 기존 트랜스포머의 연산•구조적 측면에서 Scalability를 성공적으로 이식했다고 평가할 수 있겠다.

💡 Insight 2. Pure Self-Attention은 좋은 이미지 피처를 추출하기에 충분하다

• Patch Embedding Layer의 PCA 결과, 패치의 기저가 되는 차원과 유사한 모양을 추출
  • Convolution 없이 Self-Attention만으로도 충분히 이미지의 좋은 피처를 추출하는 것이 가능
  • Vision에서 Convolution에 대한 reliance 탈피 가능

Patch Embedding Layer’s Filter

위 자료는 충분한 학습을 거치고 난 ViT의 Patch Embedding Layer의 필터를 PCA한 결과 중에서 특잇값이 높은 상위 28개의 피처를 나열한 그림이다. 이미지의 기본 뼈대가 되기에 적합해 보이는 피처들이 추출된 모습을 볼 수 있다.

따라서 Inductive Bias 없이, 단일 Self-Attention만으로 이미지의 피처를 추출하는 것이 충분히 가능하다. 비전 분야에 만연한 Convolution 의존에서 벗어나 새로운 아키텍처의 도입이 가능함을 시사한 부분이라고 할 수 있겠다.

💡 Insight 3. Bottom2General Information, Top2Specific Information

• 입력과 가까운 인코더일수록 Global & General한 Information을 포착
• 출력과 가까운 인코더일수록 Local & Specific한 Information을 포착

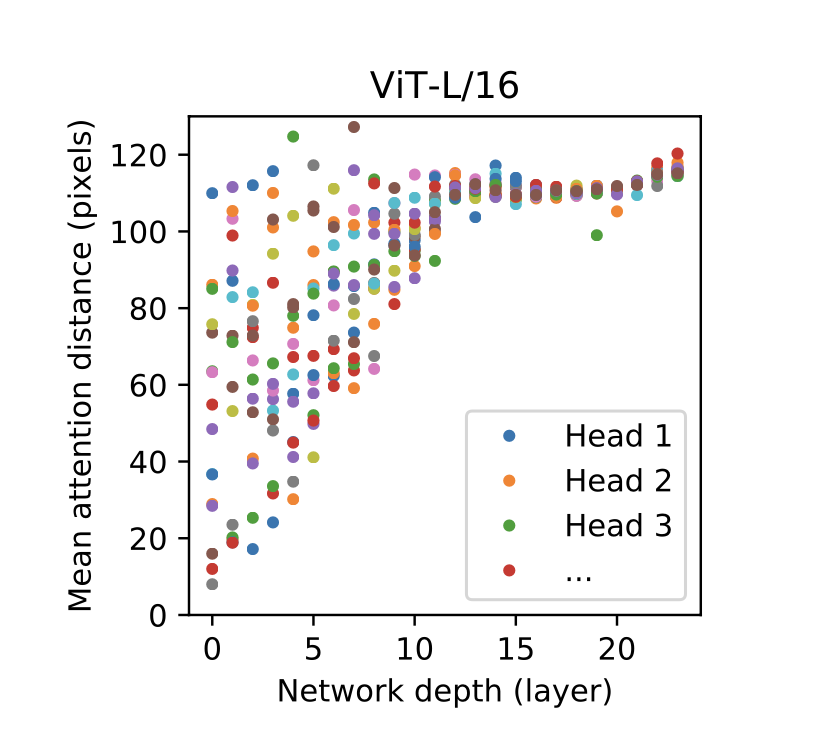Multi-Head Attention Distance per Network Depth

다음 자료는 인코더의 개수 변화에 따른 개별 어텐션 해드의 어텐션 거리 변화 추이를 나타낸 그림이다. 여기서 어텐션 거리란, 해드가 얼마나 멀리 떨어진 패치를 어텐션했는지 픽셀 단위로 표현한 지표다. 해당 값이 높을수록 거리상 멀리 떨어진 패치와 어텐션을, 작을수록 가까운 패치와 어텐션 했다는 것을 의미한다. 다시 도표를 살펴보자. 입력과 가까운 인코더일수록(Depth 0) 해드별 어텐션 거리의 분산이 커지고, 출력과 가까운 인코더일수록(Depth 23) 분산이 점자 줄어들다가 거의 한 점에 수렴하는듯한 양상을 보여준다. 다시 말해, 입력과 가까운 Bottom Encoder는 멀리 떨어진 패치부터 가까운 패치까지 모두 전역적(Global)으로 어텐션을 수행해 General 한 정보를 포착하게 되고 출력과 가까운 Top Encoder는 개별 해드들이 모두 비슷한 거리에 위치한 패치(Local)에 어텐션을 수행해 Specific 한 정보를 포착하게 된다.

이 때 Global과 Local이라는 용어 때문에 Bottom Encoder 는 멀리 떨어진 패치와 어텐션하고, Top Encoder는 가까운 패치와 어텐션한다고 착각하기 쉽다. 그러나 개별 해드들의 어텐션 거리가 얼마나 분산되어 있는가가 바로 Global, Local을 구분하는 기준이 된다. 입력부에 가까운 레이어들은 헤드들의 어텐션 거리 분산이 매우 큰 편인데, 이것을 이패치 저패치 모두 어텐션 해보고 비교해본다고 해석해서 Global이라고 부르고, 출력부에 가까운 레이어는 헤드들의 어텐션 거리 분산이 매우 작은 편인데, 이게 바로 각각의 헤드들이 어떤 정보에 주목해야할지(분류 손실이 가장 작아지는 패치) 범위를 충분히 좁힌 상태에서 특정 부분에만 집중한다는 의미로 해석해 Local 이라고 부르게 되었다.

<Revisiting Few-sample BERT Fine-tuning>도 위와 비슷한 맥락의 사실에 대해 언급하고 있으니 참고해보자. 이러한 사실은 트랜스포머 인코더 계열 모델을 튜닝할 때 Depth 별로 다른 Learning Rate을 적용하는 Layerwise Learning Rate Decay 의 초석이 되기도 한다. Layerwise Learning Rate Decay 에 대해서는 여기 포스트를 참고하도록 하자.

Output from Last Encoder

한편 논문에는 언급되지 않은, 필자의 뇌피셜에 가깝지만, 출력에 가까운 인코더들의 해드가 가진 Attention Distance이 모두 비슷하다는 사실로 이미지 분류에 결정적인 역할을 하는 피처가 이미지의 특정 구역에 모여 있으며, 그 스팟은 이미지의 중앙 부근일 가능성이 높다고 추측 해볼 수 있다. 모든 해드의 픽셀 거리가 서로 비슷하려면 일단 비슷한 위치의 패치에 어텐션을 해야하기 때문에 분류 손실값을 최소로 줄여주는 피처는 보통 한 구역(패치)에 몰려 있을 것이라고 유추가 가능하다. 또한 특정 스팟이 중앙에 위치할수록 어텐션 거리의 분산이 줄어들것이라고 생각 해볼 수도 있었다. 저자는 Attention Rollout이라는 개념을 통해 Attention Distance을 산출했다고 언급하는데, 자세한 내용은 옆에 두 링크를 참고해보자(한국어 설명 블로그, 원논문). 이러한 필자의 가설이 맞다면, Convolution 의 Inductive Bias 중 Locality 의 효과성을 Self-Attention을 통해 입증이 가능하며, 반대로 Convolution에 대한 의존에서 벗어나 단일 Self-Attention 으로도 같은 효과를 낼 수 있다는 증거 중 하나가 될 것이다.

💡 Insight 4. ViT는 CLS Pooling 사용하는게 효율적

• CLS Pooling은 GAP 보다 2배 이상 큰 학습률을 사용해도 비슷한 성능을 기록
  • 학습 속도는 더 빠르되 성능이 비슷하기 때문에 CLS Pooling 이 더 효율적

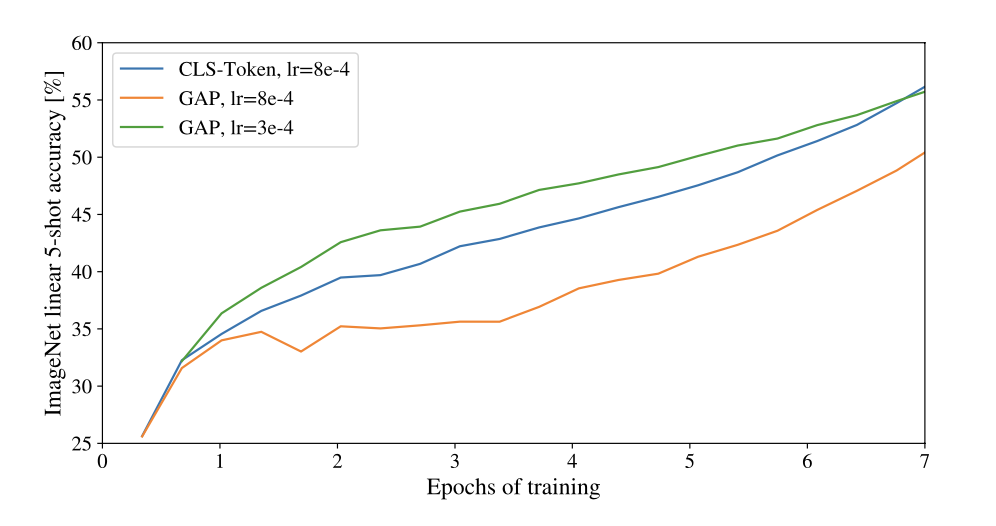Performance Trend by Pooling Method with LR

다음 도표는 풀링 방식과 학습률의 변동에 따른 정확도 변화 추이를 나타낸 그림이다. 비슷한 성능이라면 CLS Pooling이 GAP보다 2배 이상 큰 학습률을 사용했다. 학습률이 크면 모델의 수렴 속도가 빨라져 학습 속도가 빨라지는 장점이 있다. 그런데 성능까지 비슷하다면 ViT는 CLS Pooling을 사용하는 것이 더 효율적이라고 할 수 있겠다.

나중에 시간이 된다면 다른 풀링 방식, 예를 들면 Weighted Layer Pooling, GeM Pooling, Attention Pooling 같은 것을 적용해 실험해보겠다.

💡 Insight 5. ViT는 Absolute 1D-Position Embedding 사용하는게 가장 효율적

• 어떤 형태로든 위치 임베딩 값을 정의해준다면, 형태와 종류에 상관없이 거의 비슷한 성능을 보임
• 성능이 비슷하면, 직관적이고 구현이 간편한 Absolute 1D-Position Embedding 방법을 사용하는 것이 가장 효율적
• ViT는 Patch-Level 사용해, Pixel-Level보다 상대적으로 시퀀스 길이가 짧아 위치•공간 정보를 인코딩하는 방식에 영향을 덜 받음

Performance Table by making Position Embedding method

위 실험 결과는 Position Embedding 인코딩 방식에 따른 ViT 모델의 성능 변화 추이를 나타낸 자료다. 인코딩 형태와 상관없이 위치 임베딩의 유무가 성능에 큰 영향을 미친다는 사실을 알려주고 있다. 한편, 인코딩 형태 변화에 따른 유의미한 성능 변화는 없었다. 하지만 Absolute 1D-Position Embedding의 컨셉이 가장 직관적이며 구현하기 편하고 연산량이 다른 인코딩보다 적다는 것을 감안하면 ViT에 가장 효율적인 위치 임베딩 방식이라고 판단할 수 있다.

논문은 결과에 대해 ViT가 사용하는 Patch-Level Embedding이 Pixel-Level보다 상대적으로 짧은 시퀀스 길이를 갖기 때문이라고 설명한다. 예를 들어 224x224 사이즈의 이미지를 16x16 사이즈의 패치 여러장으로 만든다고 생각해보자. 임베딩 차원에 들어가는 $N$ 은 $(224/16)^2$ , 즉 196이 된다. 한편 이것을 Pixel-Level로 임베딩 하게 되면 $224^2$, 즉 50176 개의 시퀀스가 생긴다. 따라서 Pixel-Level 에 비하면 훨씬 짧은 시퀀스 길이를 갖기 때문에 Absolute 1D-Position Embedding 만으로도 충분히 Spatial Relation을 학습할 수 있는 것이다.

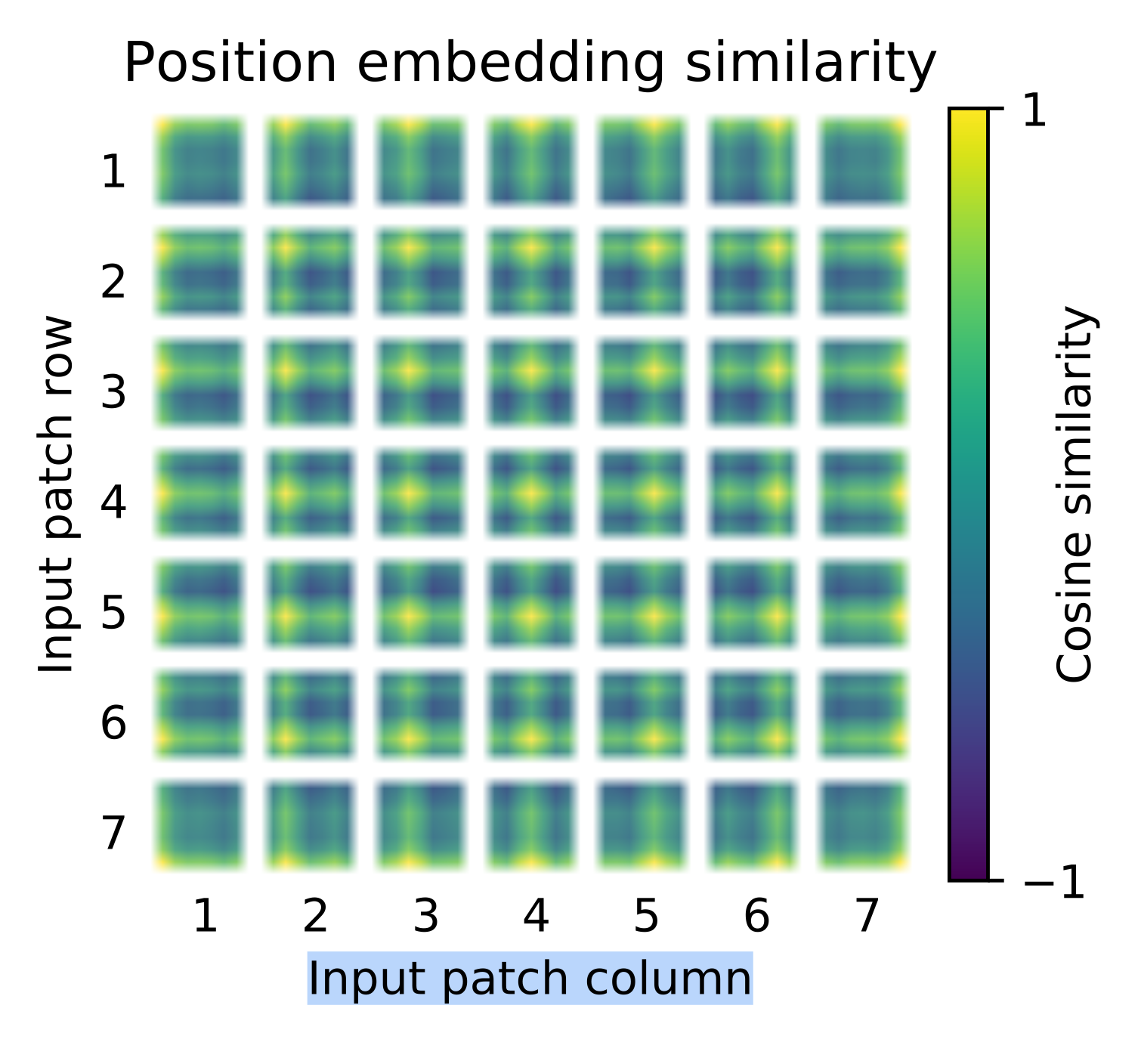Absolute 1D-Position Embedding

하지만, 필자는 자연어 처리의 Transformer-XL, XLNet, DeBERTa 같은 모델들이 Relative Position Embedding 방식을 적용해 큰 성공을 거둔 바가 있다는 점을 생각하면 이런 결과가 납득이 가면서도 의아했다.

저자는 실험에 사용한 모든 데이터 세트를 224x224로 resize 했다고 밝히고 있는데, 만약 이미지 사이즈가 512x512정도만 되더라도 $N$ 값이 1024 이라서 위 결과와 상당히 다른 양상이 나타나지 않을까 하는 생각이 든다. 추후에 시간이 된다면 이 부분도 꼭 실험해봐야겠다. 예측컨데 이미자 사이즈가 커질수록 2D Position Embedding 혹은 Relative Position Embedding이 더 효율적일 것이라 예상한다.

🧑‍⚖️ Conclusion

이렇게 ViT 모델을 제안한 <An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale>에 실린 내용을 모두 살펴보았다. Conv 에 대한 의존을 탈피 했다는 점에서 매우 의미가 있는 시도였으며, Self-Attention & Transformer 구조 채택만으로도 컴퓨터 비전 영역에 어느 정도 scalability 를 이식하는데 성공했다는 점에서 후대 연구에 중요한 시사점을 남겼다. 상대적으로 정체(??)되어 있던 비전 영역이 성능의 한계를 한단계 뛰어넘을 수 있는 초석을 마련해준 셈이다.

하지만, ViT의 Pretrain Stage에 적합한 Self-Supervised Learning 방법을 찾지 못해 여전히 Supervised Learning 방식을 채택한 점은 매우 아쉬웠다. 이는 결국 데이터 Scale 확장에 한계를 의미하기 때문이다. 오늘날 BERT와 GPT의 성공 신화는 비단 Self-Attention와 Transformer의 구조적 탁월성에 의해서만 탄생한게 아니다. 이에 못지 않게(개인적으로 제일 중요하다 생각) 주요했던 것이 바로 데이터 Scale 확장이다. MLM, AR 등의 Self-Supervised Learning 덕분에 데이터 Scale을 효율적으로 스케일 업 시킬 수 있었고, 사전 훈련 데이터의 증가는 모델 깊이, 너비, 차원까지 더욱 크케 키우는데 기여했다.

또한 ViT는 선천적으로 Patch-Level Embedding을 사용하기 때문에 다양한 이미지 테스크에 적용하는 것이 힘들다. Segmentation, Object Detection 같은 Task는 픽셀 단위로 예측을 수행해 객체를 탐지하거나 분할해야 한다. 하지만 Patch 단위로 훈련을 수행했던 ViT는 Pixel 단위의 예측을 수행하는데 어려움을 겪는다.

마지막으로 Self-Attention 자체의 Computational Overhead가 너무 심해 고해상도의 이미지를 적절히 다루기 힘들다. 위에서도 언급했지만 이미지의 사이즈가 512x512만 되어도 이미 패치의 개수가 1024가 된다. 사이즈가 커질수록 시퀀스 길이 역시 기하급수적으로 커지는데다가 Self-Attention 는 쿼리와 키 행렬을 내적 (자기 자신과 곱이라 볼 수 있음) 하기 때문에 Computational Overhead가 $N^2$이 된다.

필자는 ViT를 절반의 성공이라고 평하고 싶다. 본래 ViT의 설계 목적은 비전 분야의 Conv에 대한 의존을 탈피하면서, 퓨어한 Self-Attention을 도입해 Scalabilty 를 이식하는 것이었다. Self-Attention을 도입하는데는 성공했지만, 여전히 다룰 수 있는 이미지 사이즈나 Task에는 한계가 분명하며 결정적으로 Self-Supervised Learning 방식을 도입하지 못했다. Scalabilty 라는 단어의 의미를 생각하면, 방금 말한 부분에서까지 확장성이 있어야 설계 의도에 부합하는 결과라고 생각한다.