🔢 Vector Space: Linear Independent, Span, Sub-space, Column Space, Rank, Basis, Null Space

🔢 Linear Independent

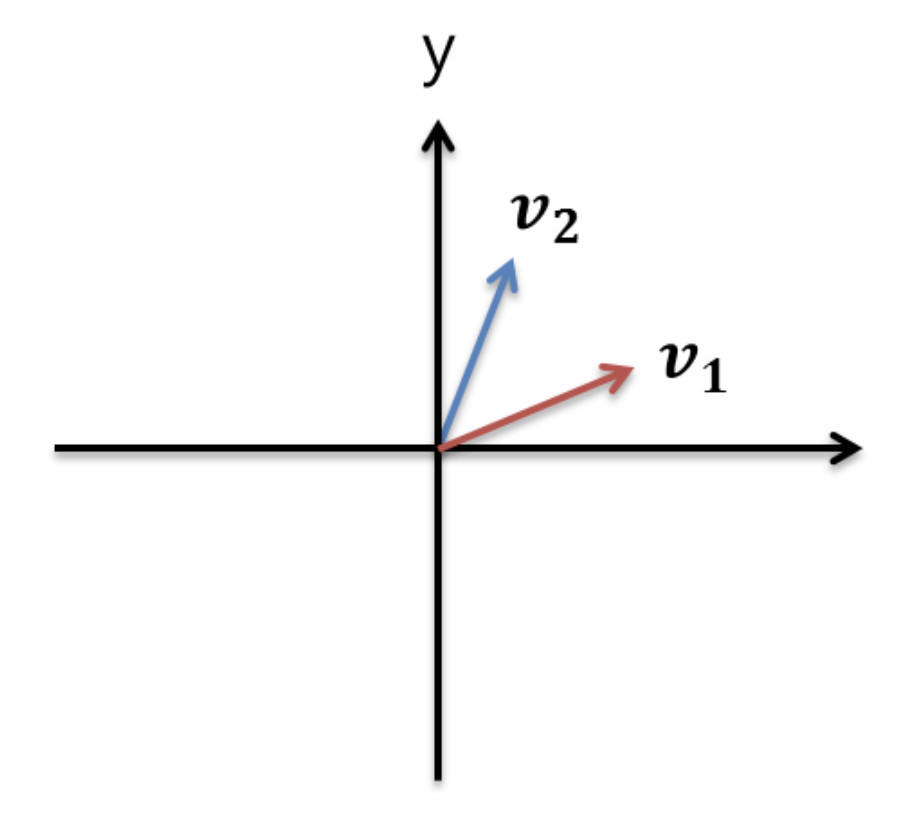
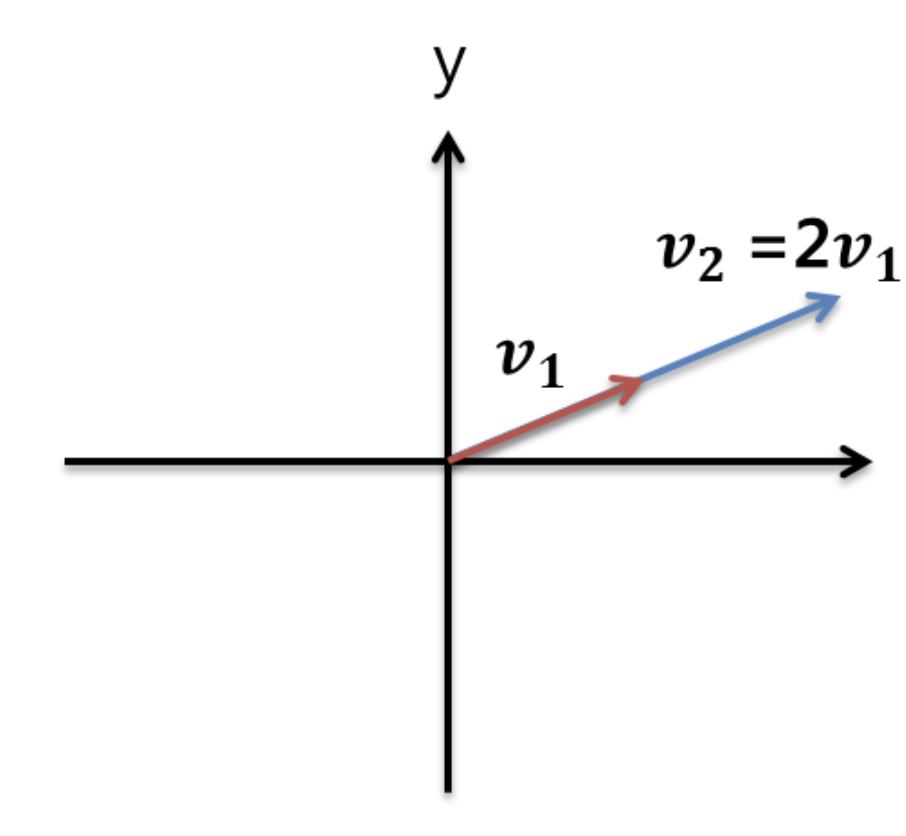
기저에 대해 알기 위해서는 먼저 linear independent(선형 독립)의 의미를 알아야 한다. 선형독립이란, 왼쪽 그림처럼 서로 다른 벡터들이 관련성 없이 독립적으로 존재하는 상태를 말한다. 따라서 서로 다른 두 벡터가 선형 독립이라면 한 벡터의 선형결합(조합)으로 다른 벡터를 표현할 수 없다. 반대로 선형 종속 상태면 오른쪽 그림처럼 벡터를 다른 벡터의 선형조합으로 표현 가능하다.

\[A\vec x = 0 \ \ \ (1)\]

어떤 벡터 $\vec x$에 대해서 위 등식을 만족하는 경우가 오직 선형변환 $A$가 영행렬일 때 밖에 없다면, 벡터 $\vec x$는 선형독립이다. 아래와 같은 벡터와 선형변환 예시를 생각해보자.

\[\vec x = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}, \ \ \ A = \begin{bmatrix} 2 \\ -1 \end{bmatrix}\]

벡터 $\vec x$에 선형결합을 해보자.

\[\begin{bmatrix} 1 \\ 2 \end{bmatrix}*2-\begin{bmatrix} 2 \\ 4\end{bmatrix} = 0\\\]

그렇다면 정확히 영벡터가 된다. 선형 종속의 의미를 잘 생각해보면, 어떤 벡터를 다른 벡터의 선형 변환으로 나타낼 수 있다면 우리는 해당 벡터의 상태를 선형 종속이라고 한다. 그렇다면 선형 독립은 이에 정반대 되는 개념일 것이다. 다시 말해, 어떤 벡터를 다른 벡터의 선형 변환 상태로 나타낼 수 없다면 우리는 해당 벡터 집합의 상태를 선형 독립이라고 한다. 따라서 (1)번 수식을 만족하는 경우가 오직 선형변환 $A$가 영행렬일 때만이라면 해당 벡터는 선형독립이라고 볼 수 있겠다.

🗂️ Span, Sub-space

Span Image

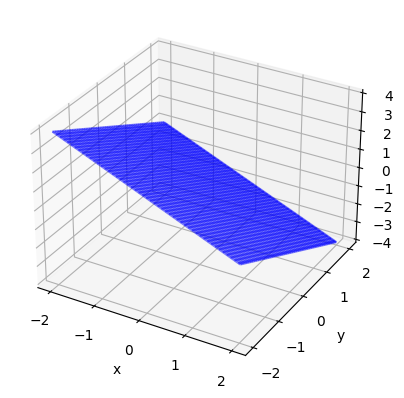
span이란, 주어진 벡터 집합을 선형 결합하여 만들 수 있는 모든 subspace을 만드는 행위를 말한다. 다시 말해, span 은 선형 결합하는 과정 자체를 나타내고 subspace 는 span의 결과물이라고 생각하면 쉽다.

span 과 subspace 을 떠올릴 때, 가장 오해하기 쉬운 부분은 바로 벡터 개수와 생성되는 부분 공간의 차원의 같다고 생각하는 점이다. 위 그림을 보자. 해당 그림은 3차원 벡터 공간에서 3개의 벡터의 벡터를 span 한 결과를 시각화한 자료다. 생성되는 subspace은 2차원 평면임을 직관적으로 알 수 있다. 왜 이런 현상이 발생했을까? 위 그림을 플롯팅하는데 사용한 벡터 집합을 보면 그 해답을 알 수 있다.

\[\begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}\]

지금까지 정리한 개념으로 위와 같은 행렬을 분석해보자. 첫번째 열벡터와 두번째 열벡터는 서로 선형독립이다. 어떤 선형결합으로도 서로를 만들어 낼 수 없다. 이것을 확장해 3개의 열벡터 중에서 임의의 어떤 두 벡터를 뽑아서 선형독립 여부를 조사해보자. 어떤 선형결합으로도 서로를 만들어낼 수 없다. 따라서 행렬 $A$는 일단 최소 2차원 평면의 공간은 부분 공간으로 만들어 낼 수 있다는 것을 알 수 있다.

이번에는 3개의 벡터 모두에 대해서 선형 독립 여부를 조사해보자. 이번에는 첫번째 열벡터와 두번째 열벡터의 선형 결합으로 3번째 벡터를 만들어 낼 수 있다. 첫번째와 세번째의 결합으로도 두번째 열벡터 생성이 가능하다. 따라서 행렬 $A$는 최대 2차원 평면의 부분 공간을 생성해낼 수 있다고 판정할 수 있겠다.

이처럼 span 으로 생성되는 subspace 차원은 서로 선형 독립인 열벡터의 개수에 의해서 결정된다는 것을 알 수 있다.

🔢 Column Space

\[C(A) = Range(A)\]

열벡터가 span하는 공간을 의미한다. span 이란, 벡터의 집합에 의해 생성된 모든 linear combination의 결과로 생성할 수 있는 부분 공간을 말한다고 언급했었다. 따라서 column space 는 열벡터의 linear combination 결과로 생성할 수 있는 vector space의 부분 공간을 말한다.

🧮 Rank

Column Space Image

행렬에서 independent한 column의 개수를 의미하며, 기하학적으로는 column space가 실제 span하는 공간의 차원을 말한다. Rank Theorem 에 의해, 행렬 $A$ column vector는 행렬 $A^T$의 row vector와 같다. 따라서 column rank와 row rank 값 역시 항상 동일하다. 행렬 $A$의 랭크는 $rank(A)$로 표기한다.

행렬의 랭크는 행렬의 생김새에 따라 부르는 명칭이 조금씩 바뀐다. 예를 들어 열벡터가 모두 선형 독립이면서 크기가 10x3 인 행렬 $C$가 있다고 가정해보자. 모든 열벡터가 선형 독립이기 때문에 우리는 행렬 $C$의 랭크가 3이라는 것을 알 수 있다. 이 때 행렬 $C$를 full-column rank 라고 부른다. 그리고 행벡터의 랭크 역시 랭크 정리 이론에 의해 3이 될 것이다. 이번에는 행렬 $C$의 열벡터 랭크가 2라고 가정해보자. 우리는 이 때 행렬 $C$를 rank-deficient로 정의한다. 만약 행렬 $C$의 열벡터가 모두 선형독립이고 그 크기가 10x10이라면 뭐라고 부를까?? 이 때는 열벡터, 행벡터 모두 랭크가 10이 되기 때문에 full-rank 라고 부른다.

정리하면 행렬의 랭크란, 행렬의 행의 크기 M 그리고 열의 크기 N 중에서 더 작은값보다 같거나 작으면서 independent한 column의 개수라는 의미를 내포한 개념이라고 볼 수 있겠다.

추가로, column vector와 row vector를 순서대로 곱하면 항상 $Rank = 1$인 행렬 $A$가 만들어진다는 것이다. 그렇게 만들어진 행렬의 원소가 두 벡터의 linear combination 으로 구성된 것이라서 당연한 소리라고 생각할 수 있지만, 이것은 선형대수학에서 매우 중요한 성질이 된다. 뒤집어서 보면 어떤 행렬의 $Rank=1$이라는 것은 그 행렬이 어떤 다른 행렬의 기본 단위 요소가 된다는 의미이기 때문이다. 어떤 행렬의 랭크가 4라는 것은 랭크 1짜리 행렬 4개의 조합이라고 생각해볼 수 있다.

🍖 Basis

이제 기저에 대해 알아보자. 기저란 선형 독립이면서 벡터 공간을 span 하는 벡터 집합을 말한다. 다시 말해, 공간 또는 차원을 표현하는데 필요한 요소들의 집합이라고 볼 수 있다. 예를 들어 2차원 공간을 표현하고 싶다면 서로 선형 독립인 벡터 2개가 필요하다. 오른쪽 그림처럼 벡터 2개가 존재해도 서로 종속 관계라면 표현(span)할 수 있는 공간은 1차원의 직선이 되기 때문이다. 정리하면, $N$차원 공간의 기저란 선형 독립이면서 벡터 공간을 span하는 벡터가 $N$개 있는 상태다. 추가로, $N$차원 공간의 기저는NxN 크기의 Invertable한 행렬과 동치를 이룬다. 뒤에서 더 자세히 다루겠지만 역행렬은 좌표평면 상에서 reverse linear combination 의 역할을 하기 때문이다.

한편 기저는 유일하지 않다. 위에서 언급한 $N$차원 기저의 필요충분조건을 만족하는 모든 벡터 집합은 모두 기저가 될 수 있다.

🦴 Standard Basis

\[I= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]

표준 기저란, 기저가 표현하는 차원의 축이 우리가 흔히 아는 x축, y축, z축 이 되는 기저 벡터를 말한다. 수학적으로는 주대각성분의 값이 모두 1인 대각행렬 $D$, 즉 단위 행렬 $I$가 기저일 때 우리는 표준 기저라고 정의한다.

👌 Null Space

\[Ax=0\]

위 수식을 만족하는 벡터 $x$의 집합을 말한다. 다시 말해, 선형 변환 $A$(크기가 MxN인 행렬)를 통해 0이 되는 벡터 집합 $x$가 바로 null space(영공간)이다. 영공간은 선형변환 $A$의 랭크와 무관하며 선형변환 A의 열차원인 $R^N$상에 존재하는 공간이다. 그래서 $Ax=0$을 행렬과 벡터의 내적으로 해석하면 영공간은 선형변환 $A$의 row space와 수직이다라는 사실을 알 수 있다.

\[N_A = dim(Null(A)) - rank(A)\]

한편, 영공간이 span 하는 공간의 차원과 션형변환 $A$의 랭크를 더하면 션형변환 $A$의 열차원을 알 수 있다. 수식으로 표현하면 다음과 같다.

🫲 Left Null Space

\[A^Tx=0\]

선형변환 $A$의 크기가 MxN일 때, $A$의 좌 영공간은 $A$의 모든 열들에 대해 선형 조합으로 0 벡터(영벡터)가 되는 모든 벡터 집합 $x$의 공간을 좌영공간이라고 한다. $A$의 열벡터에 대한 영공간이라는 것이 포인트가 된다. 따라서 좌영공간은 선형변환 $A$의 전치행렬인 $A^T$의 영공간을 구하는 것과 같으며, 선형변환 $A$의 column space와 수직하게 된다.