🔢 Product & Quotient Rule: 곱의 미분, 몫의 미분

곱의 미분, 몫의 미분은 함수가 곱의 꼴 형태 $f(x)g(x)$ 혹은 분수 꼴 형태 $\frac{f(x)}{g(x)}$를 가지고 있을 때 도함수를 구하는 방법이다. 고등학교 미적분 시간(17~18학번 기준)에 배운적이 있지만, 합성함수 미분법과 더불어 단순 암기의 폐해로 까먹기 좋은 미분법들이다. 크로스 엔트로피, 소프트맥스 미분에 쓰이므로 합성함수 미분법과 마찬가지로 딥러닝, 머신러닝에서 매우 중요하다.

✖️ Product Rule

몫의 미분은 곱의 미분의 원리를 이해하면 자동으로 알 수 있기 때문에 곱의 미분부터 살펴보겠다. 먼저 아래와 같이 곱의 형태를 가지는 함수 $p(x)$가 있다고 가정해보자.

\[p(x) = f(x)g(x)\ \ \ (0)\]

우변의 두 항을 분리하기 전에 도함수의 정의를 이용해 도함수 $p’(x)$를 구하면 다음과 같다.

\[p'(x) = \lim_{h -> 0} \frac{p(x+h) - p(x)}{h}\ \ \ (1)\]

이제 다시 $p(x+h),\ p(x)$에 $f(x)g(x)$를 대입해보자.

\[p'(x) = \lim_{h -> 0} \frac{p(x+h) - p(x)}{h} = \lim_{h->0} \frac{f(x+h)g(x+h) - f(x)(g(x)}{h}\ \ \ (2)\]

이 지점에서 우리가 뭘하려고 지금 이렇게 수식을 전개하고 있는지 상기할 필요가 있다. 우리는 곱의 형태를 갖는 함수의 도함수를 구하고 싶은 것이다. (1)번처럼 함수에 대입하는 입력값을 뺀 결과가 $h$가 되도록 말이다. (1)과 같은 꼴을 만들어주기 위해 약간의 트릭을 쓸 필요가 있다. 사용할 트릭은 대수학에서 정말 빈번하게 사용되므로 잘 기억하고 있는게 좋다. 바로 $A-A = 0$이라는 것을 이용하는 것이다. 이게 무슨 말인가는 아래 수식을 보면 알 수 있다.

\[p'(x) = \lim_{h->0} \frac{f(x+h)g(x+h) - f(x)g(x+h) + f(x)g(x+h) - f(x)g(x)}{h}\ \ \ (3)\]

(3)번 수식은 (2)번 수식의 분자에 $- f(x)g(x+h) + f(x)g(x+h)$만 추가된 형태다. 두항을 더하면 0이 되기 때문에 사실 (2)번과 (3)번은 같은 수식이라고 볼 수 있는 것이다. 그래서 두항을 추가해도 전혀 문제가 없다. 이제 우리가 익숙한 도함수 정의를 만족하는 항들이 직관적으로 보인다.

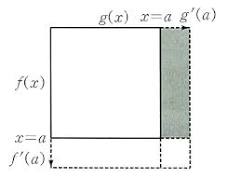
\[p'(x) = f'(x)g(x) + f(x)g'(x)\ \ \ (4)\]

따라서 수식을 정리하면 결국 곱의 형태를 갖는 함수의 도함수는 (4)번과 같은 공식을 갖게 되는 것이다. 한편, 곱의 미분법은 (0)번 수식을 직사각형의 넓이라고 간주하면 좀 더 직관적으로 이해할 수 있다. 따라서 직사각형 넓이 $p(x)$에 대한 도함수 $p’(x)$는 넓이의 순간 변화율로 해석할 수 있다.

곱의 미분의 직관적 해석

우변의 왼쪽항이 직사각형의 아래 부분의 증가하는 영역이 되고, 우측항이 회색이 칠해진 영역이 되는 것이다. 그렇다면 그림의 우측 하단에 위치한 작은 사각형의 넓이는 어떻게 처리해줘야 할까?? 곱의 미분 공식에는 해당 영역을 반영하는 항이 전혀 없다. 그 이유는 영역의 넓이가 너무나 작아서 근사치로 간주하고 무시해도 될 정도라서 그렇다. 해당 사각형의 가로 길이는 $g’(h)$, 세로 길이는 $f’(h)$가 된다. 도함수의 정의를 다시 떠올려보면 $h$는 0의 극한으로 근사하기 때문에 두 항의 곱인 영역의 넓이 역시 0에 매우 근접하게 된다. 따라서 고려할 필요 없이 무시해도 된다.

➗ Quotient Rule

몫의 미분은 곱의 미분 공식을 이용하고 나서 남은 지저분한 수식만 잘 정리하면 된다. 다음과 같이 분수 꼴 형태의 함수 $q(x)$가 있다고 가정해보자.

\[q(x) = \frac{f(x)}{g(x)} \ \ \ (0)\]

곱의 미분 공식을 이용하기 위해 분수 꼴의 함수를 다시 곱의 형태로 바꿔보자.

\[f(x) = q(x)g(x) \ \ \ (1)\]

이제 공식을 이용해 좌변에 대한 도함수를 구해보자.

\[f'(x) = q'(x)g(x) + q(x)g'(x)\ \ \ (2)\]

우리가 구하고 싶은 것은 분수 꼴을 갖는 함수 $q(x)$의 도함수 $q’(x)$이다. 따라서 (2)번 수식을 $q’(x)$에 대해서 정리해야 한다.

\[q'(x) = \frac{f'(x) - q(x)g'(x)}{g(x)}\ \ \ (3)\]

(3)번 수식을 예쁘게 정리하기 위해 공통 분모 $\frac{1}{g(x)}$를 앞으로 빼주고, $q(x)$에 (0)번 수식을 대입해 정리하면 몫의 미분법 공식, (5)번이 도출된다.

\[q'(x) = \frac{1}{g(x)}(\frac{f'(x)g(x)-f(x)g'(x)}{g(x)})\ \ \ (4) \\ q'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\ \ \ (5)\]

이렇게 곱의 미분법, 몫의 미분법의 공식이 유도되는 과정을 모두 살펴보았다.