🍎 Newton-Raphson Method for Optimization

🤔 Zero-Find Ver

비선형 방정식의 근사해를 찾거나 최적화 문제를 해결하는 방식으로, 같은 과정을 반복해 최적값에 수렴한다는 점에서 경사하강법이랑 근본이 같다. 반면, 경사하강에 비해 빠른 수렴 속도를 자랑하고 풀이 방식이 매우 간단하다는 장점이 있다. 하지만 여러 제약 조건과 더불어 해당 알고리즘이 잘 작동하는 상황이 비현실적인 부분이 많아 경사하강에 비해 자주 사용되지는 않고 있다. 뉴턴-랩슨 방식은 근사해를 찾거나, 최적화 문제를 푸는 두 가지 버젼이 있는데 먼저 해를 찾는 버전부터 살펴보자. 알고리즘의 수식은 다음과 같다.ㅂ

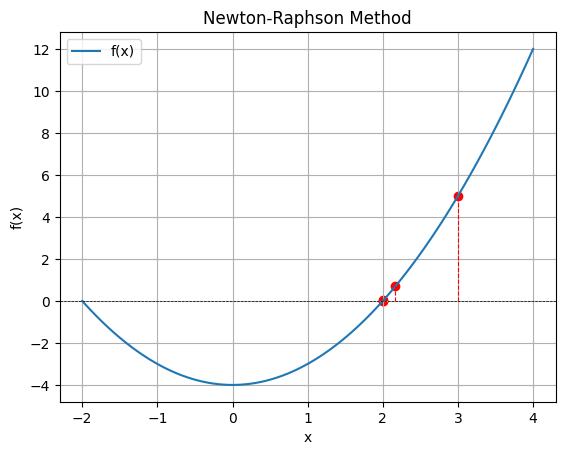
\[x_{n+1}:= x_n - \frac{f(x_n)}{f'(x_n)}\]

반복법을 사용하기 때문에 수식의 생김새가 상당히 경사하강법과 비슷하다. 왜 이런 수식이 등장하게 되었을까?? 일단 뉴턴-랩슨 방식의 풀이 과정을 살펴보자. 먼저 초기값을 설정한다. 그 다음 해당 점을 지나는 접선의 방정식을 세운다. 이제 접선의 방정식의 $x$절편을 구하고 이것을 다음 초기값으로 사용한다. 이제 $f(x_n) \approx 0$이 될 때까지 위 과정을 지속적으로 반복하면 된다. 아래 그래프와 함께 다시 살펴보자.

Newton-Raphson for Zero Find

초기값은 $x_0=3$이다. 시작점 $(x_0, f(x_0))$을 지나는 접선의 방정식을 세우고 해당 방정식의 $x$절편을 구하는 수식을 작성하면 아래와 같다.

\[f'(x_0)(x-x_n) + f(x_0) = 0\]

이제 이것을 예쁘게 잘 정리해서 다음 초기값 $x_1$을 구해보자.

\[x = x_0 - \frac{f(x_0)}{f'(x_0)}\]

이번 포스트 맨 처음에 봤던 뉴턴-랩슨 방법의 수식과 똑같다는 것을 알 수 있다. 다시 말해 뉴턴-랩슨의 Zero-Find 버전은 접선의 방정식의 $x$절편을 활용해 목적 함수의 해를 찾아가는 방식인 것이다.

지금까지 근사해를 찾아주는 뉴턴-랩슨 메서드를 살펴보았다. 하지만 머신러닝처럼 현실의 최적화 문제를 풀어야 하는 우리 입장에서는 단순 목적 함수의 근을 찾는 것만으로는 주어진 문제를 해결할 수 없다. 머신러닝의 최적화 대상인 비용 함수는 거의 모든 경우에 근이 없기(베이지안 오차까지 고려하면 사실상 불가능) 때문에 일단 알고리즘의 가정 자체가 성립하지 않는다. 이러한 한계점을 극복하고자 최적화 버전의 뉴턴-랩슨 메서드가 등장하게 된다.

📉 Optimization Ver

\[x_{n+1}:= x_n - \frac{f'(x_n)}{f''(x_n)}\]

최적화 버전의 뉴턴 랩슨 메서드는 이계도함수를 사용한다. 원함수(비용함수)가 근이 없을지라도, 함수의 극점이 존재하는한 도함수의 근은 항상 존재한다는 가정에서 출발한다. 근을 찾는 행위는 동일하게 하되, 이번에는 원함수의 근이 아니라 도함수의 근을 찾는다. 도함수의 근사해를 찾으면, 해당 위치는 국소/전역 최적값에 근접한 수치일 것이라고 기대해볼 수 있다.

하지만 최적화 버전의 뉴턴 랩슨 메서드 역시 여전히 많은 단점을 갖고 있다. 일단 먼저 계산량이 지나치게 많아진다. 예시를 모두 스칼라 형태로 들어서 간단해 보이지만, 다변수함수에 적용하면 과정이 매우 매우 복잡해진다. 모든 iteration 마다 자코비안, 헤시안 행렬을 구해줘야 한다. 도함수만 이용하는 경사 하강에 비해 연산 부담이 상당히 커질 수 밖에 없는 것이다. 그리고 결정적으로 헤시안 행렬이 invertible 해야한다. 이게 개인적으로 뉴턴-랩슨 방식의 가장 큰 단점이라고 생각한다. 헤시안 행렬의 역행렬이 존재하려면 반드시 원함수는 Convex Function이어야 하기 때문이다. 따라서 상당히 비현실적인 풀이 방식이라고 볼 수 있다.

한편, 위 모든 제약 조건을 만족한다면 최적화 버전의 뉴턴-랩슨 방식은 경사하강에 비해 상당히 빠른 수렴 속도를 갖는데 그 이유를 간단히 살펴보자. 결과부터 설명하면 뉴턴-랩슨 방식이 사실상 Least Square Method(최소 자승법) 와 동치라서 그렇다. 목적함수 $f(x)$를 MSE 로 두고 선형 회귀 문제를 푸는 상황을 가정해보자.

\[Z = Ax+n \\ f(x) = (Z-Ax)^T(Z-Ax)\]

목적함수를 정의했기 때문에 우리는 이제 목적함수의 도함수와 이계도함수를 구할 수 있다.

\[f'(x) = -2A^T(Z-Ax)\\ f''(x) = 2A^tA\]

도함수와 이계도 함수를 뉴턴—랩슨 수식에 대입하면 다음과 같다.

\[x_{n+1} := x_n + \frac{A^T(Z-Ax)} {A^TA} = x_n + (A^TA)^{-1}A^T(Z-Ax)\]

분모는 헤시안 행렬과 동치다. 행렬로 어떤 수를 나눌 수는 없기 때문에 나눗셈 표현 대신 역행렬로 표기했다. 그리고 수식이 상당히 더럽기 때문에 정리를 위해 전개를 해보려 한다. 전개 결과는 다음과 같다.

\[x_{n+1} := x_n + (A^TA)^{-1}A^TZ - (A^TA)^{-1}A^TAx_n = (A^TA)^{-1}A^TZ\]

헤시안 행렬이 invertible 해야한다라는 제약 조건이 여기서 등장한다. 만약 헤시안 행렬이 invertible 이라면, 다 날라가고 우변의 항만 남게 된다. 우변의 항을 자세히 살펴보면, Least Square Method(최소 자승법) 의 수식과 동일하다는 것을 알 수 있다. 경사하강과는 다르게 $x_n$과 관련된 항이 수식에 전혀 남아있지 않기 때문에, 최소 자승법 수식을 한 번 풀어내는 것만으로 극점에 도달하여 수렴속도가 훨씬 빠르게 되는 것이다.

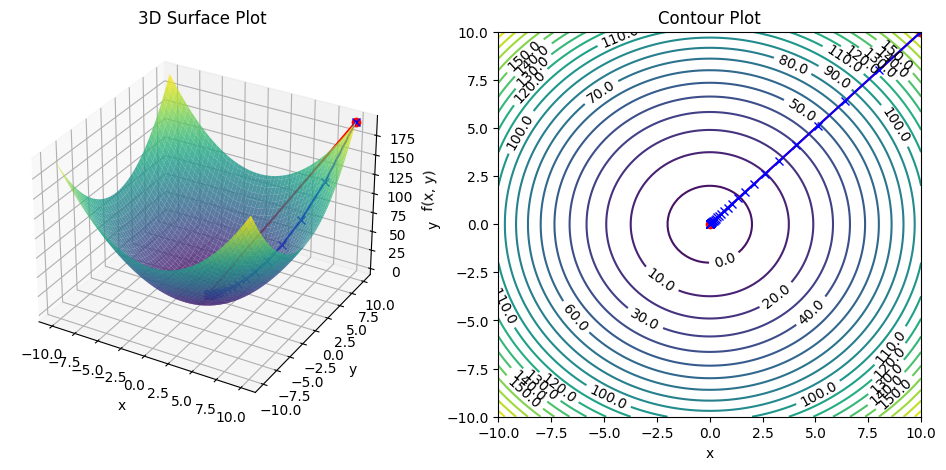Newton-Raphson for Optimization

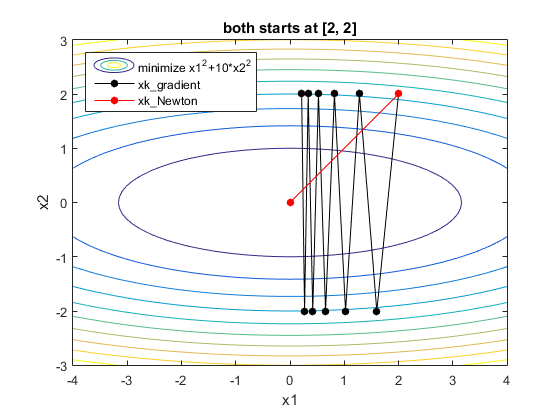
두 방식이 최적화 문제를 풀어나가는 과정을 비교하기 위해 시각화를 시도해봤다. 필자의 시각화 실력이 매우 좋지 못해 그 차이가 직관적으로 잘 안보인다… 빨간 직선은 뉴턴-랩슨 방식이고 파란 직선은 경사 하강 방법이다. 전자는 위에서 살펴본 것처럼 한번에 극소점으로 이동하는 것을 볼 수 있다. 한편 후자는 수많은 Iteration 을 거쳐 극소점에 도달한다. 필자의 시각화 자료가 상당히 좋지 못하다고 생각해 하단에 혁펜하임님의 자료도 함께 첨부했으니 참고하자. 훨씬 직관적으로 잘 보인다.

Newton-Raphson vs Gradient-Descent